
【题目】已知函数![]() .
.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若![]() 对任意的
对任意的![]() 恒成立,求满足题意的所有整数m的取值集合.
恒成立,求满足题意的所有整数m的取值集合.
【答案】(1)![]() ;(2)答案见解析;(3)
;(2)答案见解析;(3)![]() .
.
【解析】
(1)利用切点和斜率求得切线方程.
(2)求得![]() 的表达式,利用
的表达式,利用![]() ,对
,对![]() 分成
分成![]() ,
,![]() 两种情况进行分类讨论,由此求得
两种情况进行分类讨论,由此求得![]() 的单调区间.
的单调区间.
(3)由![]() 对任意的
对任意的![]() 恒成立,得到
恒成立,得到![]() 对
对![]() 成立,由此构造函数
成立,由此构造函数![]() ,利用来导数研究
,利用来导数研究![]() 的单调区间和最值,由此求得整数
的单调区间和最值,由此求得整数![]() 的取值集合.
的取值集合.
(1)![]() ,所以
,所以![]() ,
,![]() ,
,
所以所求切线方程为![]() ,即
,即![]() .
.
(2)由已知,![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),
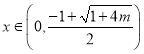 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
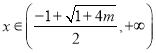 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数的单调递减区间为
时,函数的单调递减区间为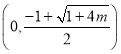 ,
,
函数的单调递增区间为 .
.
(3)由已知![]() 对
对![]() 成立,
成立,
设![]() ,
,
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
所以![]() ,
,
设![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减.
单调递减.
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以满足题意的整数m构成的集合为![]() .
.


科目:高中数学 来源: 题型:
【题目】有限数列![]() ,若满足
,若满足![]() ,
,![]() 是项数,则称
是项数,则称![]() 满足性质
满足性质![]() .
.
(1)判断数列![]() 和
和![]() 是否具有性质
是否具有性质![]() ,请说明理由.
,请说明理由.
(2)若![]() ,公比为
,公比为![]() 的等比数列,项数为10,具有性质
的等比数列,项数为10,具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)若![]() 是
是![]() 的一个排列
的一个排列![]() 都具有性质
都具有性质![]() ,求所有满足条件的
,求所有满足条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为确定数学成绩与玩手机之间的关系,从全校随机抽样调查了40名同学,其中40%的人玩手机.这40位同学的数学分数(百分制)的茎叶图如图①所示.数学成绩不低于70分为良好,低于70分为一般.
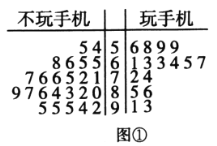
(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
数学成绩良好 | 数学成绩一般 | 总计 | |
不玩手机 | |||
玩手机 | |||
总计 | 40 |
(2)现将40名同学的数学成绩分为如下5组:
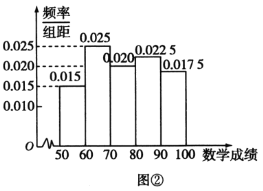
![]() ,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为
,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),求
(同一组中的数据用该组区间的中点值作代表),求![]() 与
与![]() 的误差值.
的误差值.
(3)从这40名同学数学成绩高于90分的7人中随机选取2人,求至少有一人玩手机的概率.
附:![]() ,
,
这40名同学的数学成绩总和为2998分.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是学生的必考科目,学生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生确定选考方案,否则称该学生待确定选考方案.例如学生甲选择“物理、化学和生物”三个选考科目,则称学生甲确定选考方案.某校为了解高一年级450名学生选考科目的意向,随机选取30名学生进行了一次调查,统计情况如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 有6人确定选考方案 | 0 | 1 | 2 | 6 | 6 | 3 |
有8人待确定选考方案 | 5 | 3 | 1 | 1 | 0 | 0 | |
女生 | 有10人确定选考方案 | 3 | 2 | 1 | 8 | 10 | 6 |
有6人待确定选考方案 | 5 | 4 | 1 | 0 | 0 | 1 |
(1)估计该校高一年级已确定选考方案的学生有多少人?
(2)写出确定选考方案的6名男生中选择“历史、地理和生物”的人数.(直接写出结果)
(3)从确定选考方案的6名男生中任选2名,试求出这2名学生选考科目完全相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() .
.
(2)在线段![]() 上是否存在一点
上是否存在一点![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() 四点共面?若存在,求出
四点共面?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与半椭圆
的准线与半椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 是半椭圆
是半椭圆![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒(SARS-COV-2)是2019年在人体中发现的冠状病毒新毒株,主要通过呼吸道飞沫进行传播,鉴于其特殊的传播途径,某科学医疗机构发现一次性医用口罩起着一定的防护作用一般,口罩在投入市场前需做一系列的检测,其中罩体污点、鼻梁条缺陷、耳绳异常等常规瑕疵肉眼可见,而耳绳尤为关键,会出现耳绳缺失、错位、错熔、漏熔四种情况 .现在生产商大多采用全自动生产线生产口罩,某工厂现有甲(1台本体机拖2台耳带机)和乙(1台本体机拖3台耳带机)两条生产线,已知甲生产线的日产量为7万只,乙生产线的日产量为10万只,生产商为了了解是否有必要更换原有的甲生产线,在设备生产状况相同,不计其他影响的状态下,分别统计了两条生产线生产的1000只口罩的耳绳情况,得到的统计数据如下:
耳绳情况 | 合格 | 缺失 | 错位 | 错熔 | 漏熔 |
甲生产线 | 950 | 9 | 19 | 11 | 11 |
乙生产线 | 900 | 19 | 35 | 25 | 21 |
(1)从乙生产线生产的1000只口罩中随机抽取3只,将合格品的只数记为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)假设口罩的生产成本为0.4元/只,若耳绳发生缺陷时可通过人工修复至合格来挽回损失。耳绳缺失、漏熔时人工修复费为0.01元/只;错位与错熔时需更换耳绳,其中耳绳成本为0.06元/根,人工修复费为0.02元/只.
①以修复费的平均数作为判断依据,判断哪一条生产线在每日生产过程中挽回损失时所需费用较少?
②若经一次检验就合格的口罩,生产商以1元/只的批发价销售给市场,经人工修复的打八折出售。以该工厂的日平均收入为依据分析该生产商是否有必要更换甲生产线?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com