
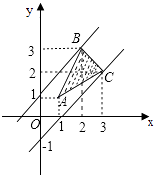
【题目】在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.
(1)若 ![]() ,求|
,求| ![]() |;
|;
(2)设 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),用x,y表示m﹣n,并求m﹣n的最大值.
(m,n∈R),用x,y表示m﹣n,并求m﹣n的最大值.
【答案】
(1)解:∵A(1,1),B(2,3),C(3,2), ![]() ,
,
∴(1﹣x,1﹣y)+(2﹣x,3﹣y)+(3﹣x,2﹣y)=0
∴3x﹣6=0,3y﹣6=0
∴x=2,y=2,
即 ![]() =(2,2)
=(2,2)
∴ ![]()
(2)解:∵A(1,1),B(2,3),C(3,2),
∴ ![]() ,
, ![]()
∵ ![]() =m
=m ![]() +n
+n ![]() ,
,
∴(x,y)=(m+2n,2m+n)
∴x=m+2n,y=2m+n
∴m﹣n=y﹣x,
令y﹣x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,
故m﹣n的最大值为1.
【解析】(1)先根据 ![]() ,以及各点的坐标,求出点p的坐标,再根据向量模的公式,问题得以解决;(2)利用向量的坐标运算,先求出
,以及各点的坐标,求出点p的坐标,再根据向量模的公式,问题得以解决;(2)利用向量的坐标运算,先求出 ![]() ,
, ![]() ,再根据
,再根据 ![]() =m
=m ![]() +n
+n ![]() ,表示出m﹣n=y﹣x,最后结合图形,求出m﹣n的最小值.
,表示出m﹣n=y﹣x,最后结合图形,求出m﹣n的最小值.
【考点精析】掌握平面向量的基本定理及其意义和平面向量的坐标运算是解答本题的根本,需要知道如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() ;坐标运算:设
;坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】用a代表红球,b代表蓝球,c代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a)(1+b)的展开式1+a+b+ab表示出来,如:“1”表示一个球都不取、“a”表示取出一个红球,而“ab”则表示把红球和蓝球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的蓝球都取出或都不取出的所有取法的是( )
A.(1+a+a2+a3+a4+a5)(1+b5)(1+c)5
B.(1+a5)(1+b+b2+b3+b4+b5)(1+c)5
C.(1+a)5(1+b+b2+b3+b4+b5)(1+c5)
D.(1+a5)(1+b)5(1+c+c2+c3+c4+c5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) 
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,圆
,圆![]() :
:![]()
![]() (
(![]() ,且
,且![]() ).
).
(1)设![]() 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆![]() 与圆
与圆![]() 的一条切线,切点分别为
的一条切线,切点分别为![]() 、
、![]() ,使得
,使得![]() ,试求出所有满足条件的点
,试求出所有满足条件的点![]() 的坐标;
的坐标;
(2)若斜率为正数的直线![]() 平分圆
平分圆![]() ,求证:直线
,求证:直线![]() 与圆
与圆![]() 总相交.
总相交.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com