
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
(1)求出![]() 在
在![]() 处的导数,利用斜率和函数值建立等式关系,则可求出
处的导数,利用斜率和函数值建立等式关系,则可求出![]() 的值. (2)由条件可知,原题等价于
的值. (2)由条件可知,原题等价于![]() 在
在![]() 上有解,设
上有解,设![]() ,即
,即![]() ,求导求函数的最值,从而求出
,求导求函数的最值,从而求出![]() 的取值范围. (3)通过求导分析
的取值范围. (3)通过求导分析![]() 的单调性和最值,分类讨论求出
的单调性和最值,分类讨论求出![]() 的取值范围.
的取值范围.
(1)![]() ,由题知
,由题知![]() ,且
,且![]() ,
,
解得![]() ;
;
(2)由(1)知![]() ,因为存在
,因为存在![]() ,使得
,使得![]() ,
,
即![]() ,设
,设![]() ,则需
,则需![]() ,
,
![]() ,设
,设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 单调递增,又因为
单调递增,又因为![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 单调递增,所以
单调递增,所以![]() ,
,
令![]() ,解得
,解得![]() ;
;
(3)![]() ,
,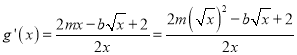 ,
,
①当![]() 时,对任意
时,对任意![]() ,易知方程
,易知方程![]() 均仅有唯一解
均仅有唯一解![]() ,
,
且当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
故方程![]() 最多有两个不同的实数解,所以
最多有两个不同的实数解,所以![]() 不符合题意;
不符合题意;
② 当![]() 时,若
时,若![]() ,则
,则![]() 恒成立,
恒成立,![]() 单调递增,
单调递增,
方程![]() 最多只有一个实数解,不符题意,
最多只有一个实数解,不符题意,
所以对任意![]() ,应有
,应有![]() ,即
,即![]() ,
,
此时,易知方程![]() 在
在![]() 上有两个不同的实数根
上有两个不同的实数根![]() ,
,
因为![]() ,不妨取
,不妨取![]() ,则有
,则有![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
由表可知,![]() 的极大值为
的极大值为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,且
,且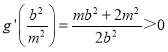 ,所以
,所以![]() ,
,
因为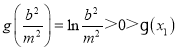 ,所以必然存在
,所以必然存在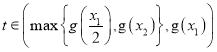 ,
,
使得方程![]() 在区间
在区间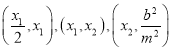 上均有一个实数解,符合题意;
上均有一个实数解,符合题意;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
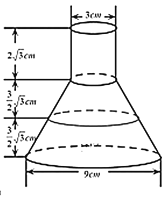
【题目】《乌鸦喝水》是《伊索寓言》中一个寓言故事,通过讲述已知乌鸦喝水的故事,告诉人们遇到困难要运用智慧,认真思考才能让问题迎刃而解的道理,如图![]() 所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为
所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为![]() 厘米,瓶底直径为
厘米,瓶底直径为![]() 厘米,瓶口距瓶颈为
厘米,瓶口距瓶颈为![]() 厘米,瓶颈到水位线距离和水位线到瓶底距离均为
厘米,瓶颈到水位线距离和水位线到瓶底距离均为![]() 厘米,现将
厘米,现将![]() 颗石子投入瓶中,发现水位线上移
颗石子投入瓶中,发现水位线上移![]() 厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
A.![]() 颗B.
颗B.![]() 颗C.
颗C.![]() 颗D.
颗D.![]() 颗
颗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
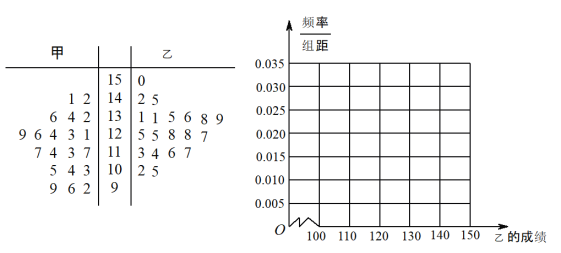
(1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩的频率分布直方图补充完整;
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在椭圆![]() 上任取一点
上任取一点![]() (
(![]() 不为长轴端点),连结
不为长轴端点),连结![]() 、
、![]() ,并延长与椭圆
,并延长与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 两点,已知
两点,已知![]() 的周长为8,
的周长为8,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设坐标原点为![]() ,当
,当![]() 不是椭圆的顶点时,直线
不是椭圆的顶点时,直线![]() 和直线
和直线![]() 的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆上,点
在椭圆上,点![]() 与点
与点![]() 关于原点对称.
关于原点对称.
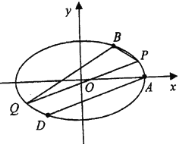
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求经过点![]() ,
,![]() 且和
且和![]() 轴相切的圆的方程;
轴相切的圆的方程;
(3)若![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]() ,
,![]() 的两个点,且
的两个点,且![]() ,点
,点![]() 在直线
在直线![]() 的上方,试判断
的上方,试判断![]() 的平分线是否经过
的平分线是否经过![]() 轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中③所示,其近月点与月球表面距离为100公里,远月点与月球表面距离为400公里,已知月球的直径约为3476公里,对该椭圆有下述四个结论:
(1)焦距长约为300公里;
(2)长轴长约为3988公里;
(3)两焦点坐标约为![]() ;
;
(4)离心率约为![]() .
.
其中正确结论的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com