
【题目】如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上. 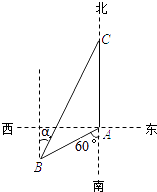
(1)求渔船甲的速度;
(2)求sinα的值.
【答案】
(1)解:依题意,∠BAC=120°,AB=12,AC=10×2=20,∠BCA=α.在△ABC中,由余弦定理,得BC2=AB2+AC2﹣2AB×AC×cos∠BAC
=122+202﹣2×12×20×cos120°=784.
解得BC=28.
所以渔船甲的速度为 ![]() 海里/小时.
海里/小时.
答:渔船甲的速度为14海里/小时
(2)解:方法1:在△ABC中,因为AB=12,∠BAC=120°,BC=28,∠BCA=α,
由正弦定理,得 ![]() .
.
即 ![]() .
.
答:sinα的值为 ![]() .
.
方法2:在△ABC中,因为AB=12,AC=20,BC=28,∠BCA=α,
由余弦定理,得 ![]() .
.
即 ![]() .
.
因为α为锐角,所以 ![]() =
= ![]() .
.
答:sinα的值为 ![]()
【解析】(1)由题意推出∠BAC=120°,利用余弦定理求出BC=28,然后推出渔船甲的速度;(2)方法一:在△ABC中,直接利用正弦定理求出sinα.方法二:在△ABC中,利用余弦定理求出cosα,然后转化为sinα.


科目:高中数学 来源: 题型:
【题目】椭圆![]() +
+![]() =1的左、右焦点分别为F1,F2,一条直线
=1的左、右焦点分别为F1,F2,一条直线![]() 经过点F1与椭圆交于A,B两点.
经过点F1与椭圆交于A,B两点.
(1)求△ABF2的周长;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,求弦长|AB|.
,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ;
;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
|
|
|
|
|
|
|
|
|
|
(1)请画出上表数据的散点图;并指出![]() 是否线性相关;
是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(3)已知该厂技术改造前![]() 吨甲产品能耗为
吨甲产品能耗为![]() 吨标准煤,试根据求出的线性回归方程,预测生产
吨标准煤,试根据求出的线性回归方程,预测生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,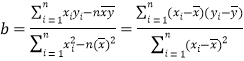 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最高点为M(
,且图象上一个最高点为M( ![]() ,3).
,3).
(1)求f(x)的解析式;
(2)先把函数y=f(x)的图象向左平移 ![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,试写出函数y=g(x)的解析式.
(3)在(2)的条件下,若总存在x0∈[﹣ ![]() ,
, ![]() ],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
],使得不等式g(x0)+2≤log3m成立,求实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0,0≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π.
(1)求f(x)的解析式;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com