Question

设集合A={x|x²-2x≤0}，B={x|a≤x≤a+1}，若B⊆A，则实数a的取值范围是________．

Answer 1

[0，1]
分析：由已知中，集合A={x|x²-2x≤0}，解二次不等式求出集合A，再由B={x|a≤x≤a+1}，若B⊆A，我们可以构造一个关于a的不等式组，解不等式组，即可得到实数a的取值范围．
解答：∵集合A={x|x²-2x≤0}=[0，2]
B={x|a≤x≤a+1}，
又∵B⊆A，
∴
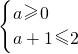
解得0≤a≤1
故实数a的取值范围是[0，1]
故答案为：[0，1]
点评：本题考查的知识点是集合关系中的参数取值问题，其中根据集合包含关系，构造出关于参数a的不等式组是解答本题的关键．