【答案】
分析:法一:由题意,可由柯西不等式得到
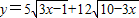
≤
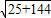
×

从而求得f(x)取得最大值,即可得答案
法二:可转化为三角函数求最值,由3x-1+10-3x=9,可令
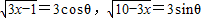
代入函数解析式得y=15cosθ+36sinθ,由三角函数的公式化简求出此三角函数的最值即可得到所求函数的最值
解答:解:法一:由柯西不等式,
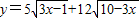
≤
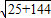
×
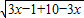
=
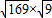
=39
当且仅当5
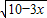
=12
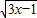
,即x=
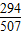
时等号成立
即x=
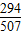
时函数取到最大值39
故答案为39
法二:由题观察到3x-1+10-3x=9,可令
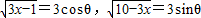
代入函数解析式得y=15cosθ+36sinθ=39(
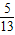
cosθ+
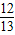
sinθ),
令tanα=
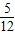
,则有sinα=
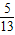
,cosα=
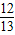
可得y=15cosθ+36sinθ=39sin(θ+α)
由于
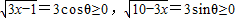
,可得
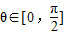
,故可得θ+α可取
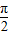
,所以有y≤39
函数的最大值为39
故答案为39
点评:本题主要考查了柯西不等式在函数极值中的应用,三角函数的最值,解答的关键是对所给函数解析式灵活变形,应用柯西不等式,或者引入参数进行三角代换,将求最值问题转化为求三角函数最值,本题第一种方法解题的重点是熟记柯西不等式,能根据题设条件直接选用或者变形后选用公式求最值,第二种解法重点是观察到3x-1+10-3x=9,即两个根式的平方和是一个常数,从而联想到三角代换,将求函数最值问题转化为求三角函数最值,在高中阶段,如本题这种类型的函数求最值不多见,若其形式这样变化
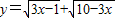
,此时函数中两个根式变量的系数互为相反数,这样的函数解析式可用基本不等式求最值,此处出现了和为定值的形式,如本题这样,由于两根式系数不相等,基本不等式不再适用,用柯西不等式即是求此类函数最值的常规方法.

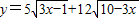 的最大值为 .
的最大值为 . 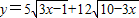 ≤
≤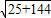 ×
× 从而求得f(x)取得最大值,即可得答案
从而求得f(x)取得最大值,即可得答案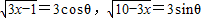 代入函数解析式得y=15cosθ+36sinθ,由三角函数的公式化简求出此三角函数的最值即可得到所求函数的最值
代入函数解析式得y=15cosθ+36sinθ,由三角函数的公式化简求出此三角函数的最值即可得到所求函数的最值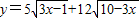 ≤
≤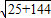 ×
×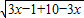 =
=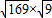 =39
=39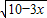 =12
=12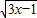 ,即x=
,即x=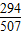 时等号成立
时等号成立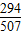 时函数取到最大值39
时函数取到最大值39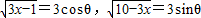
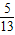 cosθ+
cosθ+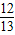 sinθ),
sinθ),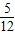 ,则有sinα=
,则有sinα=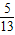 ,cosα=
,cosα=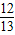
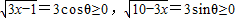 ,可得
,可得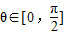 ,故可得θ+α可取
,故可得θ+α可取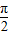 ,所以有y≤39
,所以有y≤39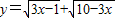 ,此时函数中两个根式变量的系数互为相反数,这样的函数解析式可用基本不等式求最值,此处出现了和为定值的形式,如本题这样,由于两根式系数不相等,基本不等式不再适用,用柯西不等式即是求此类函数最值的常规方法.
,此时函数中两个根式变量的系数互为相反数,这样的函数解析式可用基本不等式求最值,此处出现了和为定值的形式,如本题这样,由于两根式系数不相等,基本不等式不再适用,用柯西不等式即是求此类函数最值的常规方法. 

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案