
【题目】平面内与两定点![]() ,
,![]() 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数![]() 的点的轨迹,加上
的点的轨迹,加上![]() 、
、![]() 两点所成的曲线
两点所成的曲线![]() 可以是圆、椭圆或双曲线,给出以下四个结论:①当
可以是圆、椭圆或双曲线,给出以下四个结论:①当![]() 时,曲线
时,曲线![]() 是一个圆;②当
是一个圆;②当![]() 时,曲线
时,曲线![]() 的离心率为
的离心率为![]() ;③当
;③当![]() 时,曲线
时,曲线![]() 的渐近线方程为
的渐近线方程为![]() ;④当曲线
;④当曲线![]() 的焦点坐标分别为
的焦点坐标分别为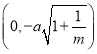 和
和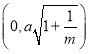 时,
时,![]() 的范围是
的范围是![]() .其中正确的结论序号为_______.
.其中正确的结论序号为_______.
【答案】①③
【解析】
设出动点![]() 的坐标,根据斜率之积为
的坐标,根据斜率之积为![]() 可求得动点的轨迹方程.依次代入
可求得动点的轨迹方程.依次代入![]() 的值可判断①②③;讨论当
的值可判断①②③;讨论当![]() 分别取
分别取![]() 和
和![]() 时焦点坐标,求得都为
时焦点坐标,求得都为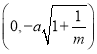 和
和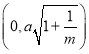 ,因而可判断④.
,因而可判断④.
设动点![]()
当![]() 时,
时,![]()
即![]() ,化简可得
,化简可得![]()
又因为![]() ,
,![]() 满足
满足![]()
所以动点![]() 的轨迹方程为
的轨迹方程为![]()
当![]() 时,曲线
时,曲线![]() 的方程为
的方程为![]() ,为圆心在原点,半径为
,为圆心在原点,半径为![]() 的圆,所以①正确;
的圆,所以①正确;
当![]() 时,曲线
时,曲线![]() 的方程为
的方程为![]() ,可化为
,可化为 ,为焦点在
,为焦点在![]() 轴上的椭圆,所以
轴上的椭圆,所以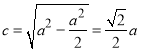 ,则离心率为
,则离心率为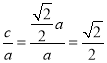 ,所以②错误;
,所以②错误;
当![]() 时,曲线
时,曲线![]() 的方程为
的方程为![]() ,可化为
,可化为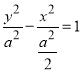 ,为焦点在
,为焦点在![]() 轴上的双曲线,所以渐近线方程为
轴上的双曲线,所以渐近线方程为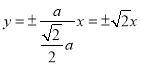 ,所以③正确;
,所以③正确;
当![]() 时,曲线
时,曲线![]() 的方程可化为
的方程可化为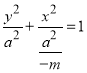 ,表示焦点在
,表示焦点在![]() 轴上的椭圆,则
轴上的椭圆,则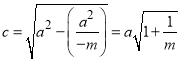 ,则焦点坐标为
,则焦点坐标为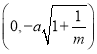 和
和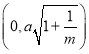 .
.
当![]() 时,曲线
时,曲线![]() 的方程可化为
的方程可化为 ,表示焦点在
,表示焦点在![]() 轴上的双曲线,则
轴上的双曲线,则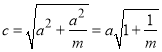 ,则焦点坐标为
,则焦点坐标为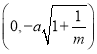 和
和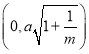 .由以上可知,当焦点坐标为
.由以上可知,当焦点坐标为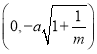 和
和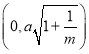 时,
时,![]() 的取值范围为
的取值范围为![]() ,所以④错误.
,所以④错误.
综上可知,正确的序号有①③
故答案为: ①③


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,过点F作斜率为k的直线l与抛物线交于A,B两点,与准线交于点P,设点D为抛物线准线与x轴的交点.
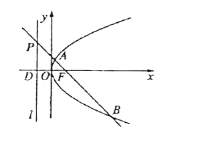
(1)若k=﹣1,求△DAB的面积;
(2)若![]() λ
λ![]() ,
,![]() μ
μ![]() ,证明:λ+μ为定值.
,证明:λ+μ为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
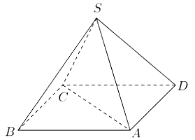
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主须为机动车购买的险种.若普通![]() 座以下私家车投保交强险第一年的费用(基本保费)是
座以下私家车投保交强险第一年的费用(基本保费)是![]() 元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
类型 | 浮动因素 | 浮动比率 |
| 上一年度未发生有责任的道路交通事故 | 下浮 |
| 上两年度未发生有责任的道路交通事故 | 下浮 |
| 上三年度未发生有责任的道路交通事故 | 下浮 |
| 上一年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一年度发生两次及以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上三年度发生有责任涉及死亡的道路交通事故 | 上浮 |
据统计,某地使用某一品牌![]() 座以下的车大约有
座以下的车大约有![]() 辆,随机抽取了
辆,随机抽取了![]() 辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
以这![]() 辆该品牌汽车的投保类型的频率视为概率,按照我国《机动车交通事故责任保险条例》汽车交强险价格为
辆该品牌汽车的投保类型的频率视为概率,按照我国《机动车交通事故责任保险条例》汽车交强险价格为![]() 元.
元.
(1)求得知,并估计该地本年度使用这一品牌![]() 座以下汽车交强险费大于
座以下汽车交强险费大于![]() 元的辆数;
元的辆数;
(2)试估计该地使用该品牌汽车的一续保人本年度的保费不超过![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主须为机动车购买的险种.若普通![]() 座以下私家车投保交强险第一年的费用(基本保费)是
座以下私家车投保交强险第一年的费用(基本保费)是![]() 元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
元,在下一年续保时,实行费率浮动制,其保费与上一年度车辆发生道路交通事故情况相联系,具体浮动情况如下表:
类型 | 浮动因素 | 浮动比率 |
| 上一年度未发生有责任的道路交通事故 | 下浮 |
| 上两年度未发生有责任的道路交通事故 | 下浮 |
| 上三年度未发生有责任的道路交通事故 | 下浮 |
| 上一年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一年度发生两次及以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上三年度发生有责任涉及死亡的道路交通事故 | 上浮 |
某一机构为了研究某一品牌![]() 座以下投保情况,随机抽取了
座以下投保情况,随机抽取了![]() 辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
辆车龄满三年的该品牌同型号私家车的下一年续保情况,统计得到如下表格:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
以这![]() 辆该品牌汽车的投保类型的频率视为概率.
辆该品牌汽车的投保类型的频率视为概率.
(I)试估计该地使用该品牌汽车的一续保人本年度的保费不超过![]() 元的概率;
元的概率;
(II)记![]() 为某家庭的一辆该品牌车在第四年续保时的费用,求
为某家庭的一辆该品牌车在第四年续保时的费用,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数的比为
内的男生数与女生数的比为![]() ,若在满意度评分值为
,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com