
【题目】某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并分别加以统计,得到如图所示的频率分布直方图.
,并分别加以统计,得到如图所示的频率分布直方图.
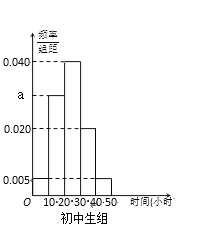
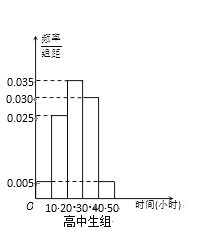
(Ⅰ)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(Ⅱ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.
【答案】(Ⅰ)![]() ;870人 (Ⅱ)
;870人 (Ⅱ)![]()
【解析】
(Ⅰ)根据频率频率直方图的性质可求得![]() 的值;由分层抽样求得初中生有60名,高中有
的值;由分层抽样求得初中生有60名,高中有
40名,再求阅读时间不小于30小时的学生的频率及人数再求和即得解;
(Ⅱ)利用古典概型的概率公式求至少抽到1名高中生的概率.
(Ⅰ)解:由频率直方图的性质,![]() ,所以
,所以![]() ,
,
由分层抽样,知抽取的初中生有60名,高中生有40名.
因为初中生中,阅读时间不小于30个小时的学生频率为![]() ,
,
所以所有的初中生中,阅读时间不小于30个小时的学生约有![]() 人,
人,
同理,高中生中,阅读时间不小于30个小时的学生频率为![]() ,学生人数约有
,学生人数约有![]() 人.
人.
所以该校所有学生中,阅读时间不小于30个小时的学生人数约有![]() 人.
人.
(Ⅱ)解:记“从阅读时间不足10个小时的样本学生中随机抽取2人,至少抽到1名高中生”为事件![]() ,
,
初中生中,阅读时间不足10个小时的学生频率为![]() ,样本人数为
,样本人数为![]() 人.
人.
高中生中,阅读时间不足10个小时的学生频率为![]() ,样本人数为
,样本人数为![]() 人.
人.
记这3名初中生为![]() ,这2名高中生为
,这2名高中生为![]() ,
,
则从阅读时间不足10个小时的样本学生中随机抽取2人,所有可能结果有10种,即:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而事件![]() 的结果有7种,它们是
的结果有7种,它们是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 内恰有一个零点,求
内恰有一个零点,求![]() 的取值范围;
的取值范围;
(3)设![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)求这5天的平均发芽率;
(2)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,用
,用![]() 的形式列出所有的基本事件,并求满足
的形式列出所有的基本事件,并求满足![]() 的事件
的事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
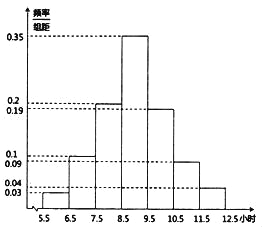
(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆C:![]() (a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=
(a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=![]() 与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com