
 ,
, ,且x∈[0,π],令函数
,且x∈[0,π],令函数
 ,
, ,且x∈[0,π],函数
,且x∈[0,π],函数 ,根据向量的数量积运算公式,我们易求出函数的解析式,并根据除幂公式,辅助角公式,可将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,得到f(x)的递增区间
,根据向量的数量积运算公式,我们易求出函数的解析式,并根据除幂公式,辅助角公式,可将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,得到f(x)的递增区间 +
+ =
= (2分)
(2分) (4分)
(4分) (5分)
(5分)
 得:
得: ∴
∴ (6分)
(6分)

 ∴
∴ (8分)
(8分) ∴
∴ (12分)
(12分)

科目:高中数学 来源:2012-2013学年江西省赣州市上犹县三中高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 ,
, .且x
.且x
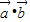 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.查看答案和解析>>
科目:高中数学 来源:2009年重庆市渝中区求精中学高一(下)期末数学试卷2(解析版) 题型:解答题
 ,
, .且x
.且x
 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江西省吉安市白鹭洲中学高二(上)期中数学试卷(解析版) 题型:解答题
 ,
, ,且x∈[0,π],令函数
,且x∈[0,π],令函数
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:4.3 两角和与差、二倍角的公式2(解析版) 题型:解答题
 ,
, .且x
.且x
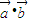 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com