
【题目】数列![]() 满足
满足![]() 对任意的
对任意的![]() 恒成立,
恒成立,![]() 为其前
为其前![]() 项的和,且
项的和,且![]() .
.
(1)求数列![]() 的通项
的通项![]() ;
;
(2)数列![]() 满足
满足![]() ,其中
,其中![]() .
.
①证明:数列![]() 为等比数列;
为等比数列;
②求集合![]() .
.
【答案】(1) ![]() (2) ①见证明;②
(2) ①见证明;②![]()
【解析】
(1)设等差数列{an}的公差为d.根据a4=4,前8项和S8=36.可得数列{an}的通项公式;
(2)①设数列{bn}前n项的和为Bn.根据bn=Bn﹣Bn﹣1,数列{bn}满足![]() .建立关系即可求解;
.建立关系即可求解;
②由![]() ,得
,得![]() ,即
,即![]() .记
.记![]() ,由①得,
,由①得,![]() ,
,
由![]() ,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由
,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由![]() ,得
,得![]() .
.
讨论整数成立情况即可;
(1)设等差数列![]() 的公差为
的公差为![]() ,因为等差数列满足
,因为等差数列满足![]() ,前8项和
,前8项和![]()
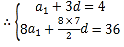 ,解得
,解得![]()
所以数列![]() 的通项公式为
的通项公式为![]()
(2)①设数列![]() 的前项和为
的前项和为![]() ,由(1)及
,由(1)及![]() 得
得
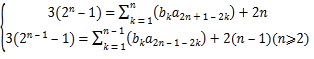
上两式相减,得到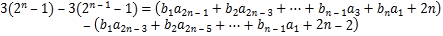
=![]()
![]()
![]()
所以![]()
又![]() ,所以
,所以![]() ,满足上式,
,满足上式,
所以![]()
当![]() 时,
时,![]()
两式相减,得![]() ,
,![]() ,
,
所以![]() 所以此数列为首项为1,公比为2的等比数列.
所以此数列为首项为1,公比为2的等比数列.
②由![]() ,得
,得![]() ,即
,即![]() ,∴
,∴![]() .
.
令![]() ,显然
,显然![]() ,此时
,此时![]() 变为
变为![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,
时,![]() ,符合题意,此时
,符合题意,此时![]() ;
;
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
下证当![]() ,
,![]() 时,方程
时,方程![]() :
:
∵![]()
∴![]()
∴![]() ,显然
,显然![]() ,从而
,从而![]()
当![]() ,
,![]() 时,方程
时,方程![]() 没有正整数解.
没有正整数解.
综上所述:![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
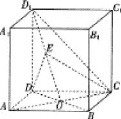
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
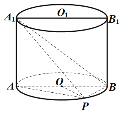
【题目】如图,已知点![]() 在圆柱
在圆柱![]() 的底面圆
的底面圆![]() 上,
上,![]() 为圆
为圆![]() 的直径.
的直径.
(1)若圆柱![]() 的体积
的体积![]() 为
为![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角(用反三角函数值表示结果);
所成的角(用反三角函数值表示结果);
(2)若圆柱![]() 的轴截面是边长为2的正方形,四面体
的轴截面是边长为2的正方形,四面体![]() 的外接球为球
的外接球为球![]() ,求
,求![]() 两点在球
两点在球![]() 上的球面距离.
上的球面距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,圆
,圆![]() .
.
(1)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(2)有一动圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com