
【题目】某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰.因库房限制每天最多加工6箱.
(1)若某天此鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且6箱该种玫瑰被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,求恰好一位是以2000元价格购买的顾客且另一位是以1200元价格购买的顾客的概率:
(2)此鲜花批发店统计了100天该种玫瑰在每天下午3点以前的销售量t(单位:箱),统计结果如下表所示(视频率为概率):
t/箱 | 4 | 5 | 6 |
频数 | 30 | x | s |
①估计接下来的一个月(30天)该种玫瑰每天下午3点前的销售量不少于5箱的天数并说明理由;
②记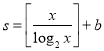 ,
,![]() ,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,
,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,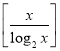 为
为![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ).
).
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)根据古典概型概率公式计算可得;
(2)①用10030可得;
②用购进5箱的平均利润>购进6箱的平均利润,解不等式可得.
解:(1)设这6位顾客是A,B,C,D,E,F.其中3点以前购买的顾客是A,B,C,D.3点以后购买的顾客是E,F.
从这6为顾客中任选2位有15种选法:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),其中恰好一位是以2000元价格购买的顾客,另一位是以1200元价格购买的顾客的有8种:(A,E),(A,F),(B,E),(B,F),(C,E),(C,F),(D,E),(D,F).
根据古典概型的概率公式得![]() ;
;
(2)①依题意![]() ,
,
∴![]() ,
,
所以估计接下来的一个月(30天)内该种玫瑰每天下午3点以前的销售量不少于5箱的天数是![]() 天;
天;
②批发店毎天在购进4箱数量的玫瑰时所获得的平均利润为:
4×20004×500×3=2000元;
批发店毎天在购进5箱数量的玫瑰时所获得的平均利润为:
![]() 元;
元;
批发店毎天在购进6箱数量的玫瑰时所获得的平均利润为:
![]()
![]()
由![]() ,
,
解得:![]() ,
,
则![]()
所以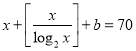 ,要求b的最小值,则求
,要求b的最小值,则求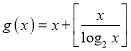 的最大值,
的最大值,
令![]() ,则
,则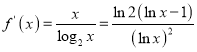 ,
,![]()
明显![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
则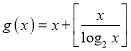 在
在![]() 上单调递增,
上单调递增,
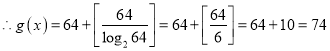 ,
,
则b的最小值为![]() .
.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
【题目】实验中学从高二级部中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1个相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级6名选手,现从每个班级6名选手中随机抽取3人回答这个问题已知这6人中,甲班级有4人可以正确回答这道题目,而乙班级6人中能正确回答这道题目的概率每人均为![]() ,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
(1)求甲、乙两个班级抽取的6人都能正确回答的概率;
(2)分别求甲、乙两个班级能正确回答题目人数的期望![]() 和方差
和方差![]() 、
、![]() ,并由此分析由哪个班级代表学校参加大赛更好?
,并由此分析由哪个班级代表学校参加大赛更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图1所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
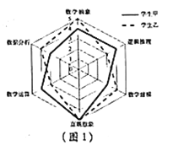
A. 乙的逻辑推理能力优于甲的逻辑推理能力
B. 甲的数学建模能力指标值优于乙的直观想象能力指标值
C. 乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D. 甲的数学运算能力指标值优于甲的直观想象能力指标值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则关于x的方程
,则关于x的方程![]() 有以下结论,其中正确的结论为( )
有以下结论,其中正确的结论为( )
A.当![]() 时,方程
时,方程![]() 恒有实根
恒有实根
B.当![]() 时,方程
时,方程![]() 在
在![]() 内有两个不等实根
内有两个不等实根
C.当![]() 时,方程
时,方程![]() 在
在![]() 内最多有9个不等实根
内最多有9个不等实根
D.若方程![]() 在
在![]() 内的实根的个数为偶数,则所有实根之和为
内的实根的个数为偶数,则所有实根之和为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,设
,设![]() 是
是![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上动点![]() 与两个定点
与两个定点![]() ,
, ![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为圆
为圆![]() 上一动点,圆心
上一动点,圆心![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 只有一个公共点
只有一个公共点![]() ,且点
,且点![]() 在第二象限,过坐标原点
在第二象限,过坐标原点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com