
【题目】对于集合![]() ,若存在两个数列
,若存在两个数列![]() 满足(i)
满足(i) ![]() ;(ii)
;(ii) ![]() ,则称M为一个“友谊集”,称(A,B)为
,则称M为一个“友谊集”,称(A,B)为![]() 的一种“友谊排列”,如A=(3,10,7,9,6)和B=(2,8,4,5,1)便是集合
的一种“友谊排列”,如A=(3,10,7,9,6)和B=(2,8,4,5,1)便是集合![]() 的一种友谊排列,记为
的一种友谊排列,记为![]()
(1)证明:若![]() 为一个友谊集,则存在偶数种友谊排列;
为一个友谊集,则存在偶数种友谊排列;
(2)确定集合![]() 及
及![]() 的全体友谊排列.
的全体友谊排列.
【答案】(1)见解析;(2)见解析
【解析】
(1)由题设对![]() 的任意一种友谊排列(A,B),作(A,B)的对偶排列
的任意一种友谊排列(A,B),作(A,B)的对偶排列![]() ,其中,
,其中,![]() ,
,![]() .
.
显然,![]() 也是M的一种友谊排列,且若
也是M的一种友谊排列,且若![]() 则
则![]() .
.
再证![]() .
.
事实上,假若![]() ,则由
,则由![]() ,得
,得![]() ,矛盾.
,矛盾.
从而,![]() 的所有友谊排列可分成若干个对偶排列组,每组两个.
的所有友谊排列可分成若干个对偶排列组,每组两个.
因此,![]() 的友谊排列有偶数种.
的友谊排列有偶数种.
(2)设![]() 的友谊排列为
的友谊排列为![]() .
.
则![]() .
.
又![]() ,
,
以上两式相减得![]() . ①
. ①
显然,![]() 而
而![]() .
.
于是,由式①得![]() 只有三种情况:
只有三种情况:![]() .
.
![]() 则
则![]() .
.
由于![]() ,于是,A中的元素8只能与B中的元素7搭配.
,于是,A中的元素8只能与B中的元素7搭配.
而A中的元素6只与B中的元素2或3搭配,
因此,只有两种排列![]() .
.
![]() ,则
,则![]() .
.
于是,A中的元素7、8只能与B中的元素4或6搭配,也只有两种排列
![]() .
.
![]() 则
则![]() .
.
于是,A中的元素2只能与B中的元素1搭配,8只能与4或5搭配,只有两种排列
![]() .
.
因此,![]() 共有6种友谊排列.
共有6种友谊排列.
同理,![]() 共有10种友谊排列:
共有10种友谊排列:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】口袋中放有20个球,其中白球9个、红球5个、黑球6个,现从中任取10个球,使得白球不少于![]() 个不多于7个,红球不少于2个不多于5个、黑球不多于3个的取法种数是( )
个不多于7个,红球不少于2个不多于5个、黑球不多于3个的取法种数是( )
A. 14 B. 24
C. 13 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“难度系数”反映试题的难易程度,难度系数越大,题目得分率越高,难度也就越小.“难度系数”的计算公式为![]() ,其中,
,其中,![]() 为难度系数,
为难度系数,![]() 为样本平均失分,
为样本平均失分,![]() 为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度系数 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
测试后,随机抽取了50名学生的数据进行统计,结果如下:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
实测平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根据试卷2的难度系数估计这480名学生第2套试卷的平均分;
(2)从抽样的50名学生的5套试卷中随机抽取2套试卷,记这2套试卷中平均分超过96分的套数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试卷的预估难度系数和实测难度系数之间会有偏差.设![]() 为第
为第![]() 套试卷的实测难度系数,并定义统计量
套试卷的实测难度系数,并定义统计量![]() ,若
,若![]() ,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个四面体,若存在一个侧面(其所在平面为![]() ),使得在将其余三个侧面分别绕其位于平面
),使得在将其余三个侧面分别绕其位于平面![]() 上的边向体外方向旋转至平面
上的边向体外方向旋转至平面![]() 上时,四个侧面在平面
上时,四个侧面在平面![]() 上共同组成的图形恰好是一个三角形,则称该四面体是一个“平展四面体”.若有一个平展四面体,它的一个侧面的三边长为a、b、c,试确定a、b、c的关系,并求该四面体的体积(用a、b、c表示).
上共同组成的图形恰好是一个三角形,则称该四面体是一个“平展四面体”.若有一个平展四面体,它的一个侧面的三边长为a、b、c,试确定a、b、c的关系,并求该四面体的体积(用a、b、c表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则取它的项:第一次取1;第二次取2个连续偶数2,4;第三次取3个连续奇数5,7,9;第四次取4个连续偶数10,12,14,16;第五次取5个连续奇数17,19,21,23,25,按此规律取下去,得到一个子数列1,2,4,5,7,9,10,12,14,16,17,19…,则在这个子数中第2014个数是( )
A. 3965 B. 3966 C. 3968 D. 3989
查看答案和解析>>
科目:高中数学 来源: 题型:
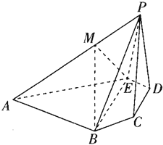
【题目】如图,已知五棱锥P-ABCDE,其中![]() ABE,
ABE,![]() PCD均为正三角形,四边形BCDE为等腰梯形,BE=2BC=2CD=2DE=4,PB=PE=
PCD均为正三角形,四边形BCDE为等腰梯形,BE=2BC=2CD=2DE=4,PB=PE=![]() .
.
(Ⅰ)求证:平面PCD⊥平面ABCDE;
(Ⅱ)若线段AP上存在一点M,使得三棱锥P-BEM的体积为五棱锥P-ABCDE体积的![]() ,求AM的长.
,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com