
分析 先根据行列式运算公式得到x2-x-m-1<0在[-1,1]上恒小于0,分离参数得到m>x2-x-1在[-1,1]上恒成立,设f(x)=x2-x-1求得其最大值,再由恒成立的原理求解即得.
解答 解:∵$|\begin{array}{l}{x}&{1}\\{m+1}&{x-1}\end{array}|$=x(x-1)-(m+1)=x2-x-m-1,
∴x2-x-m-1<0在[-1,1]上恒小于0,
∴m>x2-x-1在[-1,1]上恒成立,
设f(x)=x2-x-1=(x-$\frac{1}{2}$)2-$\frac{5}{4}$,
∴函数f(x)[-1,$\frac{1}{2}$]上单调递减,在($\frac{1}{2}$,1]上单调递增,
∴当x=-1时,函数f(x)有最大值,即f(-1)=1+1-1=1,
∴m>1,
故m的取值范围为(1,+∞),
故答案为:(1,+∞)
点评 本题主要考查二次函数求最值及不等式恒成立问题,恒成立问题往往转化为函数求最值问题解决.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
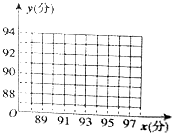 一次考试中,五名学生的数学、物理成绩如下表所示:
一次考试中,五名学生的数学、物理成绩如下表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com