
【题目】某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=(1+ ![]() )百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.
)百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.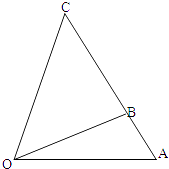
(1)试将y表示成x的函数,并求出函数y的解析式;
(2)当x取何值时?整个中转站的占地面积S△OAC最小,并求出其面积的最小值.
【答案】
(1)
解:结合图形可知,S△BOC+S△AOB=S△AOC.
于是, ![]() x(1+
x(1+ ![]() )sin30°+
)sin30°+ ![]() y(1+
y(1+ ![]() )sin45°=
)sin45°= ![]() xysin75°,
xysin75°,
解得:y= ![]() ,(其中3≤x≤6)
,(其中3≤x≤6)
(2)
解:由(1)知,y= ![]() (3≤x≤6),
(3≤x≤6),
因此,S△AOC= ![]() xysin75°
xysin75°
= ![]()
![]()
= ![]() [(x﹣2)+
[(x﹣2)+ ![]() +4]
+4]
≥2+2 ![]() (当且仅当x﹣2=
(当且仅当x﹣2= ![]() ,即x=4时,等号成立).
,即x=4时,等号成立).
∴当x=400米时,整个中转站的占地面积S△OAC最小,最小面积是(2+2 ![]() )×104平方米.
)×104平方米.
【解析】(1)由图形知,S△BOC+S△AOB=S△AOC , 代入面积公式,求出函数y的解析式;(2)由(1)知,函数y的解析式,求出S△AOC的表达式,利用基本不等式求出S△OAC最小时,x的取值以及最小面积是什么.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知集合 ![]() ,设f:x→2x﹣3是集合C={﹣1,1,n}到集合B={﹣5,﹣1,3}的映射.
,设f:x→2x﹣3是集合C={﹣1,1,n}到集合B={﹣5,﹣1,3}的映射.
(1)若m=5,求A∩C;
(2)若﹣2∈A,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017镇江一模20】已知函数![]() ,
,![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数h(x)=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
A.关于直线x=0对称
B.关于直线x=π对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,2)对称
,2)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017年第二次全国大联考江苏卷】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 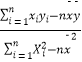 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com