
 分) 2010年11月在广州召开亚
分) 2010年11月在广州召开亚 运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平
运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平 均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均
均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均 销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).科目:高中数学 来源:不详 题型:解答题
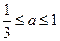 ,若函数
,若函数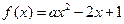 在区间
在区间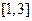 上
上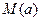 ,最小值为
,最小值为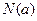 ,令
,令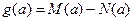 .
. 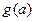 的函数表达式;
的函数表达式;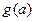 在区间
在区间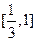 上的单调性,并求出
上的单调性,并求出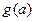 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
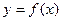
 与直线
与直线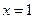 的交点个数为0或l;
的交点个数为0或l;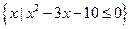 ,B={
,B={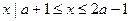 },若B
},若B 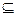 A,则-3
A,则-3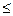 a
a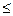 3;
3;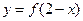 与函数
与函数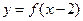 的图象关于直线
的图象关于直线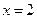 对称;
对称;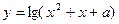 的值域为R的充要条件是:
的值域为R的充要条件是: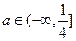 ;
;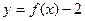 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为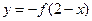 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com