
【题目】若正数x,y满足15x﹣y=22,则x3+y3﹣x2﹣y2的最小值为 .
【答案】1
【解析】解:由正数x,y满足15x﹣y=22,可得y=15x﹣22>0,则x> ![]() ,y>0, 又x3+y3﹣x2﹣y2=(x3﹣x2)+(y3﹣y2),
,y>0, 又x3+y3﹣x2﹣y2=(x3﹣x2)+(y3﹣y2),
其中y3﹣y2+ ![]() y=y(y2﹣y+
y=y(y2﹣y+ ![]() )=y(y﹣
)=y(y﹣ ![]() )2≥0,
)2≥0,
即y3﹣y2≥﹣ ![]() y,
y,
当且仅当y= ![]() 时取得等号,
时取得等号,
设f(x)=x3﹣x2 , f(x)的导数为f′(x)=3x2﹣2x=x(3x﹣2),
当x= ![]() 时,f(x)的导数为
时,f(x)的导数为 ![]() ×(
×( ![]() ﹣2)=
﹣2)= ![]() ,
,
可得f(x)在x= ![]() 处的切线方程为y=
处的切线方程为y= ![]() x﹣
x﹣ ![]() .
.
由x3﹣x2≥ ![]() x﹣
x﹣ ![]() (x﹣
(x﹣ ![]() )2(x+2)≥0,
)2(x+2)≥0,
当x= ![]() 时,取得等号.
时,取得等号.
则x3+y3﹣x2﹣y2=(x3﹣x2)+(y3﹣y2)≥ ![]() x﹣
x﹣ ![]() ﹣
﹣ ![]() y≥
y≥ ![]() ﹣
﹣ ![]() =1.
=1.
当且仅当x= ![]() ,y=
,y= ![]() 时,取得最小值1.
时,取得最小值1.
故答案为:1.
由题意可得x> ![]() ,y>0,又x3+y3﹣x2﹣y2=(x3﹣x2)+(y3﹣y2),求出y3﹣y2≥﹣
,y>0,又x3+y3﹣x2﹣y2=(x3﹣x2)+(y3﹣y2),求出y3﹣y2≥﹣ ![]() y,当且仅当y=
y,当且仅当y= ![]() 时取得等号,设f(x)=x3﹣x2 , 求出导数和单调区间、极值和最值,即可得到所求最小值.
时取得等号,设f(x)=x3﹣x2 , 求出导数和单调区间、极值和最值,即可得到所求最小值.


科目:高中数学 来源: 题型:
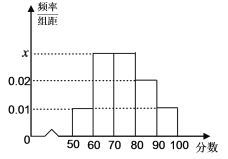
【题目】2018年高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试,现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(Ⅰ)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
(Ⅱ)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取2人参加这次考试的考后分析会,试求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1﹣BC1﹣B1的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一枚骰子掷一次得到2点的概率为![]() ,这说明一枚骰子掷6次会出现一次2点
,这说明一枚骰子掷6次会出现一次2点
B. 某地气象台预报说,明天本地降水的概率为70%,这说明明天本地有70%的区域下雨,30%的区域不下雨
C. 某中学高二年级有12个班,要从中选2个班参加活动,由于某种原因,一班必须参加,另外再从二至十二班中选一个班,有人提议用如下方法:掷两枚骰子得到的点数是几,就选几班,这是很公平的方法
D. 在一场乒乓球赛前,裁判一般用掷硬币猜正反面来决定谁先打球,这应该说是公平的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)(文科)求三棱锥![]() 的体积.
的体积.
(理科)求二面角![]() 平面角正切值的大小.
平面角正切值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.点E是CD边的中点,点F,G分别在线段AB,BC上,且AF=2FB,CG=2GB.

(1)证明:PE⊥FG;
(2)求二面角PADC的正切值;
(3)求直线PA与直线FG所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,耨市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了20户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324.
对应的家庭收入数据如下:0.21,0.24,0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83,0.93,0.97,0.96,1.1,1.2,1.5,1.8.

(1)根据国家发改委的指示精神,该市计划实施3阶阶梯电价,使75%的用户在第一档,电价为0.56元/![]() ;
;![]() 的用户在第二档,电价为0.61元/
的用户在第二档,电价为0.61元/![]() ;
;![]() 的用户在第三档,电价为0.86元/
的用户在第三档,电价为0.86元/![]() ;试求出居民用电费用
;试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系式;
间的函数关系式;
(2)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数)
的回归直线方程(回归直线方程的系数四舍五入保留整数)![]() ;
;
(3)小明家的月收入7000元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为.
的斜率和截距的最小二乘法估计分别为.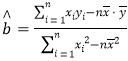 ,
,![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com