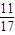分析:(1)n=1时,2s
1=a
1(a
1+1),s
1=a
1,a
1>0,解得a
1=1;n≥2时,a
n=s
n-s
n-1,2s
n=a
n(a
n+1),2s
n-1=a
n-1(a
n-1+1),作差整理得(a
n+a
n-1)(a
n-a
n-1-1)=0.由此能求出a
n.
(2)由b
n+1-b
n=
| n+1 |
 |
| i=1 |
-
| n |
 |
| i=1 |
=
| n+1 |
 |
| i=1 |
-
| n |
 |
| i=1 |
=
-=>0,能够证明无穷数列{b
n}为递增数列.
(3)由
b3=++>,知若存在正整数k,必有k≥7.有
bn=| n |
 |
| i=1 |
=
bn=| n |
 |
| i=1 |
=
bn=| 2n |
 |
| i=1 |
-| n |
 |
| i=1 |
=
| 2n |
 |
| i=1 |
-2| n |
 |
| i=1 |
=
| n |
 |
| i=1 |
.当n≥4时,由
| n |
 |
| i=4 |
<
| n |
 |
| i=4 |
,知
| n |
 |
| i=1 |
---<| n |
 |
| i=2 |
--.由此能导出存在正整数k使得
bn<对任意正整数n恒成立,且k的最小值为7.
解答:解:(1)n=1时,2s
1=a
1(a
1+1),s
1=a
1,a
1>0,
解得a
1=1.
n≥2时,a
n=s
n-s
n-1,
2s
n=a
n(a
n+1),2s
n-1=a
n-1(a
n-1+1),
作差得2a
n=a
n(a
n+1)-a
n-1(a
n-1+1),
整理得(a
n+a
n-1)(a
n-a
n-1-1)=0,
∵a
n>0,
∴a
n+a
n-1≠0,
∴a
n-a
n-1=1,
对n≥2时恒成立,因此数列{a
n}是首项为1,公差为1的等差数列,
故a
n=n;
(2)∵b
n+1-b
n=
| n+1 |
 |
| i=1 |
-
| n |
 |
| i=1 |
=
| n+1 |
 |
| i=1 |
-
| n |
 |
| i=1 |
=
+-=
-=>0,
对任意正整数n恒成立∴无穷数列{b
n}为递增数列.
(3)存在,且k的最小值为7.
∵
b3=++>,
∴若存在正整数k,
必有k≥7.
又
bn=| n |
 |
| i=1 |
=
bn=| n |
 |
| i=1 |
=
bn=| 2n |
 |
| i=1 |
-| n |
 |
| i=1 |
=
| 2n |
 |
| i=1 |
-2| n |
 |
| i=1 |
=
| n |
 |
| i=1 |
-| n |
 |
| i=1 |
=
| n |
 |
| i=1 |
(-)=
| n |
 |
| i=1 |
当n≥4时,
∵
| n |
 |
| i=4 |
<
| n |
 |
| i=4 |
∴
| n |
 |
| i=1 |
---<| n |
 |
| i=2 |
--即
| n |
 |
| i=1 |
<| n |
 |
| i=2 |
+∴2
bn=2| n |
 |
| i=1 |
=2
| n |
 |
| i=1 |
<| n |
 |
| i=1 |
+
| n |
 |
| i=2 |
+=
| 2n |
 |
| i=2 |
(-)+<
| 2n |
 |
| i=2 |
(-)+=
1-+<∴
bn<;
因此存在正整数k使得
bn<对任意正整数n恒成立,
且k的最小值为7.
点评:本题考查数列与不等式的综合利用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.













































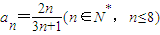 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)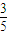 (2)
(2)