
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 为平行四边形,其中
为平行四边形,其中![]() ,
,![]() ,
,![]() ,等边
,等边![]() 所在平面与平面
所在平面与平面![]() 垂直,
垂直,![]() 平面
平面![]() ,且
,且![]() .
.
(Ⅰ)点![]() 在棱
在棱![]() 上,且
上,且![]() ,
,![]() 为
为![]() 的重心,求证:
的重心,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
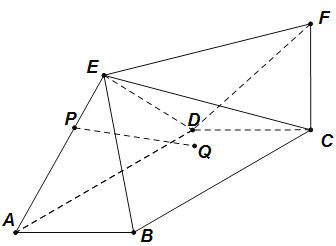
【答案】见解析
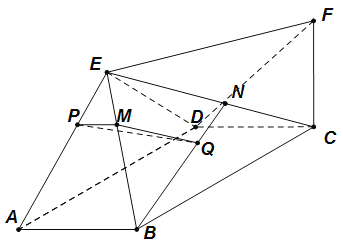
【解析】(Ⅰ)如图,在棱![]() 上取点
上取点![]() ,使得
,使得![]() ;连接
;连接![]() 并延长,交
并延长,交![]() 于点
于点![]() .
.
则在![]() 中,又
中,又![]() ,
,
所以![]() ,
,
又四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
所以![]() . -----------------2分
. -----------------2分
在![]() 中,
中,![]() 为重心,
为重心,
所以![]() ,
,
又![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() . -----------------------------5分
. -----------------------------5分
(Ⅱ)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理可得![]()
![]()
![]() .
.
所以![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
在![]() 中,
中,![]() ,
,
所以![]() ,且
,且![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() . -----------------------------7分
. -----------------------------7分
又![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,且
,且![]() .
.
如图,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
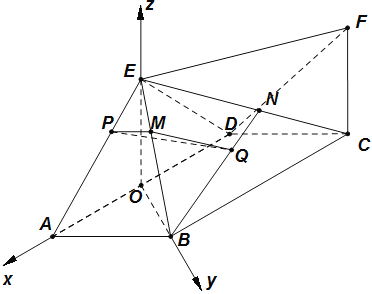
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由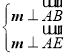 ,可得
,可得
整理得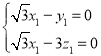 .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() 为平面
为平面![]() 的一个法向量. ----------------------------9分
的一个法向量. ----------------------------9分
设平面![]() 的法向量为
的法向量为![]() ,
,
则由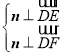 ,可得
,可得 .
.
整理得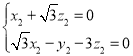 .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() 为平面
为平面![]() 的一个法向量. -----------------------------10分
的一个法向量. -----------------------------10分
所以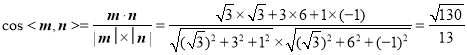 .
.
-----------------------------11分
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则![]() . -------12分
. -------12分
【命题意图】本题考查空间中线面平行的证明、空间二面角的求解以及向量的基本运算等,考查基本的空间想象能力和逻辑推理能力、运算能力等.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合M满足M{1,2,3},且M中至少有一个奇数,这样的集合M有6个;
②已知函数f(x)= ![]() 的定义域是R,则实数a的取值范围是(﹣12,0);
的定义域是R,则实数a的取值范围是(﹣12,0);
③函数f(x)=loga(x﹣3)+1(a>0且a≠1)图象恒过定点(4,2);
④已知函数f(x)=x2+bx+c对任意实数t都有f(3+t)=f(3﹣t),则f(1)>f(4)>f(3).
其中正确的命题序号是(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 过点A(2,1),离心率为
过点A(2,1),离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() 与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且
与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且![]() ,求直线l的方程.
,求直线l的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若![]() ,求
,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

(1)令![]() ,利用给出的参考数据求出
,利用给出的参考数据求出![]() 关于
关于![]() 的回归方程
的回归方程![]() .(
.(![]() ,
,![]() 精确到0.1)
精确到0.1)
参考数据:![]() ,
,![]() ,
,![]()
其中![]() ,
,![]()
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年新高一学生入学后,为了了解新生学业水平,某区对新生进行了素质测查,随机抽取了50名学生的数学成绩(均低于100分),其相关数据统计如下:
分数段 | 频数 | 选择题≥24分 |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(1)若全区高一新生有5000人,试估计成绩不低于60分的人数;
(2)根据表格数据试估计全区新生数学的平均成绩(同一分数段的数据取该区间的中点值作为代表,如区间![]() 的中点值为75);
的中点值为75);
(3)从成绩在![]() 中抽取选择题得分不低于24分的3名学生进行具体分析,求至少有2名学生成绩在
中抽取选择题得分不低于24分的3名学生进行具体分析,求至少有2名学生成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com