
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为
【答案】
(1){1,2,4}
(2)2m+1﹣1
【解析】解:由题意可得,ap+aq=ak , 其中p、q、k∈N* ,
由等差数列的通向公式可得a1+(p﹣1)d+a1+(q﹣1)d=a1+(k﹣1),
整理得d= ![]() ,(1)若a1=4,则d=
,(1)若a1=4,则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,
故d的取值集合为 {1,2,4};(2)若a1=2m(m∈N*),则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,…,2m ,
∴d的所有可能取值的和为1+2+4+…+2m= ![]() =2m+1﹣1,
=2m+1﹣1,
所以答案是(1){1,2,4},(2)2m+1﹣1.
【考点精析】本题主要考查了等比数列的前n项和公式和等差数列的性质的相关知识点,需要掌握前![]() 项和公式:
项和公式: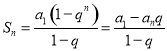 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 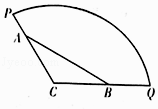
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在射线y=2x﹣3(x≥0),且与直线y=x+2和y=﹣x+4都相切.
(1)求圆C的方程;
(2)若P(x,y)是圆C上任意一点,求x+2y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式(x+5)(3﹣2x)≤6的解集是( )
A.{x|x≤﹣1或x ![]() }
}
B.{x|﹣1≤x ![]() }?
}?
C.{x|x ![]() 或x≥﹣1}
或x≥﹣1}
D.{x| ![]() ?x≤﹣1}
?x≤﹣1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据3,4,5,a,b的平均数是4,中位数是m,从3,4,5,a,b,m这组数据中任取一数,取到数字4的概率为 ![]() ,那么3,4,5,a,b这组数据的方差为( )
,那么3,4,5,a,b这组数据的方差为( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】儿童乘坐火车时,若身高不超过1.1m,则不需买票;若身高超过1.1m但不超过1.4m,则需买半票;若身高超过1.4m,则需买全票.试设计一个买票的算法,并写出相应的程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式ax2+bx+c<0的解集为({﹣∞,﹣1})∪( ![]() ,+∞),则不等式cx2﹣bx+a<0的解集为( )
,+∞),则不等式cx2﹣bx+a<0的解集为( )
A.(﹣1,2)
B.(﹣∞,﹣1)∪(2,+∞)
C.(﹣2,1)
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com