
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
图1:甲套设备的样本的频率分布直方图

表1:乙套设备的样本的频数分布表
质量指标数 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格 | |||
不合格 | |||
合计 |
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]() 其中
其中![]()
【答案】(1)见解析;(2)没有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
【解析】
(1)根据图1和表1中的数据,分别求出甲、乙的合格率,再比较合格率的大小及各区间产品的分布情况即可;
(2)根据图1和表1中的数据,可求得甲、乙的合格和不合格的产品数量,即可完成列联表,将表中的数据代入![]() 的公式,求出
的公式,求出![]() ,查对临界值作出判断,即可得到结论.
,查对临界值作出判断,即可得到结论.
(1)根据图1和表1可知:甲套设备生产的合格品概率约为![]() ,
,
乙套设备生产的合格品的概率约为![]() ;
;
乙设备生产的产品的质量指标主要集中在![]() 之间,
之间,
甲套设备生产的产品的质量指标与乙设备相比较为分散;
因此,可以认为乙套设备生产的合格品的概率更高,且质量指标更稳定,从而乙套设备优于甲套设备.
(2)根据表1和图1可得列联表:
甲套设备 | 乙套设备 | 合计 | |
合格 |
|
|
|
不合格 |
|
|
|
合计 |
|
|
|
提出假设![]() :该企业生产的这种产品的质量指标值与甲、乙两套设备的选择无关.
:该企业生产的这种产品的质量指标值与甲、乙两套设备的选择无关.
根据联表中的数据可以求得
![]() ,
,
当![]() 成立时,
成立时,![]() 的概率大于
的概率大于![]() ,
,
故没有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上两人所得与下三人等。问各得几何?”其意思是:“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得之和与丙、丁、戊三人所得之和相等,且甲、乙、丙、丁、戊所得依次成等差数列。问五人各得多少钱?”(“钱”是古代的一种重量单位)。这个问题中,戊所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C.
钱 C. ![]() 钱 D.
钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .下列命题正确的为_______________.
.下列命题正确的为_______________.
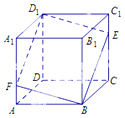
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,![]() ,其相邻的两个1被2隔开,第
,其相邻的两个1被2隔开,第![]() 对1之间有
对1之间有![]() 个2,则数列的前209项的和为( )
个2,则数列的前209项的和为( )
A. 279 B. 289 C. 399 D. 409
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某建筑物内一个水平直角型过道如图所示.两过道的宽度均为![]() ,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为
,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为![]() ,长为
,长为![]() ,试问:该设备能否水平移进直角型过道?
,试问:该设备能否水平移进直角型过道?
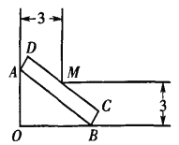
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为迎接中华人民共和国成立![]() 周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:
周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:

(1)扇形统计图中三等奖所在扇形的圆心角的度数是__________度;
(2)请补全条形统计图;
(3)在此次征文比赛中,获得“一等奖”的同学中有两人来自初三年级.现要从获得“一等奖”同学中随机抽选两人参加该校团委组织的征文比赛总结会,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:x2+y2+2kx+(4k+10)y+10k+20=0,其中k≠-1.
(1)求证:曲线C都表示圆,并且这些圆心都在同一条直线上;
(2)证明:曲线C过定点;
(3)若曲线C与x轴相切,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是正项数列{an}的前n项和,满足a1=2,anan+1=6Sn﹣2,n∈N*.
(1)求证:{an}是等差数列;
(2)记bn=2n,求数列{|an﹣bn|}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com