Question

袋中有5个白球，3个黑球，从中任意摸出4个，求下列事件发生的概率：
（1）摸出2个或3个白球；
（2）至少摸出1个白球；
（3）至少摸出1个黑球．

Answer 1

【答案】分析：（1）先写出试验发生的总事件数有C₈⁴种不同的结果，再写出摸出2个或3个白球包含的事件数，求比值即可．
（2）对于至少或至多的问题一般从它的对立事件来考虑，摸出的是四个黑球．
（3）做法同第二问一样，也可以从它的对立事件来考虑，本题的这一问可以换一下问法．
解答：解：从8个球中任意摸出4个共有C₈⁴种不同的结果．
记从8个球中任取4个，其中恰有1个白球为事件A₁，
恰有2个白球为事件A₂，3个白球为事件A₃，4个白球为事件A₄，恰有i个黑球为事件B_i．
则（1）摸出2个或3个白球的概率
P₁=P（A₂+A₃）=P（A₂）+P（A₃）=+=+=．
（2）至少摸出1个白球的概率
P₂=1-P（B₄）=1-0=1．
（3）至少摸出1个黑球的概率
P₃=1-P（A₄）=1-=．
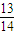
点评：本题这种类型是近几年高考题中经常出现的，考查古典概型，大型考试中文科考试必出的一道问题．理科一般出离散型随机变量的分布列和期望．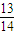