(12分)(Ⅰ)已知直线
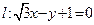
,求
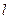
关于
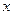
轴对称的直线方程;
(Ⅱ)已知圆
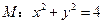
,求过点
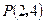
与圆
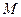
相切的切线方程
(1)
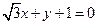
(2)
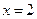
解:(Ⅰ)(法1)∵所求直线与
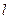
关于
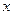
轴对称
又
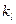
=
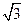
∴所求直线斜率为-
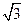
∵直线
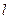
与
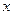
轴交于点(-
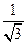
,0)
∴所求直线为
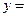
-
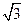
(
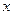
+
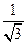
)
即
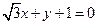
…………………6分
(Ⅰ)(法2)在直线
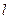
上取两点(0,1),(
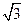
,4)
∵所求直线与
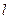
关于
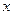
轴对称
∴点(0,-1)和(
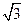
,-4)在所求直线上
∴所求直线的斜率为
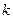
=-
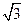
∴所求直线为
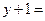
-
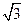
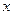
即
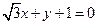
…………………6分
(Ⅱ)∵点
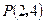
不在圆
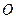
上
∴可设切线
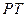
为
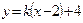
∵
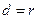
∴
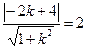
解得
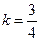
……………………9分
∴
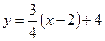
即
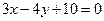
…………………11分
∵过圆外一点作圆的切线应该有两条
∴另一条直线的斜率不存在
易求另一条切线为
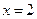
…………
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分9分)
已知

关于
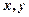
的方程
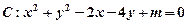
.
(Ⅰ)若方程
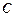
表示圆,求
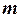
的取值范围;
(Ⅱ)若圆
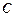
与直线
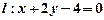
相交于
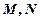
两点,且
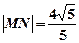
,求
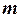
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知点M(1,0)是圆C:
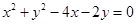
内的一点,则过点M的最短弦
所在的直线方程是( )
A
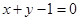
B
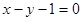
C
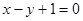
D
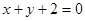
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
如图,圆
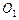
与圆
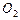
的半径

都等于1,
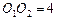
. 过动点
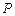
分别作圆
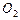
、圆
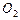
的切线
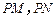
(
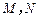
分别为切点),使得|PM|=|PN|.
试建立适当的坐标系,并求动点
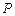
的轨迹方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
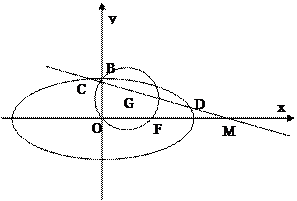
(本小题满分12分)如图,已知圆
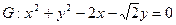
经过椭圆
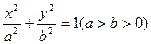
的右焦点F及上顶点B.过点
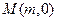
作倾斜角为
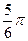
的直线
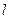
交椭圆于C、D两点.
(1)求椭圆的方程;
(2)若点
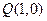
恰在以线段CD为直径
的圆的内

部,求实数
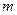
范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知实数r是常数,如果
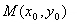
是圆
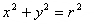
内异于圆心的一点,那么直线
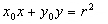
与圆
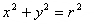
的位置关系是( )
| A.相交但不经过圆心 | B.相交且经过圆心 |
| C.相切 | D.相离 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(文科)设直线
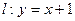
与椭圆
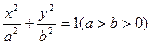
相交于
A、
B两个不
同的点,与
x轴相交于点
F.
(I)证明:
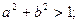
(II)若
F是椭圆的一个焦点,且
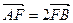
,求椭圆的方程。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
若直线
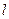
过点
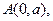
斜率为1,圆
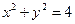
上恰有3个点到
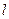
的距离为1,
则
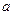
的值为××××××.
查看答案和解析>>

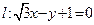 ,求
,求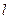 关于
关于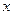 轴对称的直线方程;
轴对称的直线方程;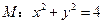 ,求过点
,求过点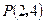 与圆
与圆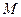 相切的切线方程
相切的切线方程 一线名师权威作业本系列答案
一线名师权威作业本系列答案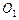 与圆
与圆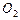 的半径
的半径 都等于1,
都等于1,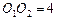 . 过动点
. 过动点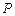 分别作圆
分别作圆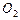 、圆
、圆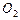 的切线
的切线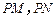 (
(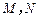 分别为切点),使得|PM|=|PN|.
分别为切点),使得|PM|=|PN|. 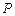 的轨迹方程.
的轨迹方程.
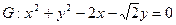 经过椭圆
经过椭圆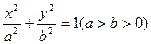 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点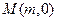 作倾斜角为
作倾斜角为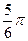 的直线
的直线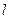 交椭圆于C、D两点.
交椭圆于C、D两点.
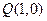 恰在以线段CD为直径
恰在以线段CD为直径 部,求实数
部,求实数 范围.
范围.