
【题目】已知函数![]() (
(![]() ).
).
(1)若函数![]() 是单调函数,求
是单调函数,求![]() 的取值范围;
的取值范围;
(2)求证:当![]() 时,都有
时,都有![]() .
.
【答案】(1)![]() 或
或![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)对函数求导,由函数![]() 是单调函数可得
是单调函数可得![]() 或
或![]() 在
在![]() 上恒成立,利用分离参数的方法,当
上恒成立,利用分离参数的方法,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,分别求右端的最值或极限值即可;(2)由(1)可知,当
,分别求右端的最值或极限值即可;(2)由(1)可知,当![]() 时,
时, ![]() 在
在![]() 上递减,根据单调性化简可得
上递减,根据单调性化简可得![]() 成立,利用分析法将所证命题转化为
成立,利用分析法将所证命题转化为![]() ,构造函数
,构造函数![]() ,求出
,求出![]() 即可.
即可.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵函数![]() 是单调函数,∴
是单调函数,∴![]() 或
或![]() 在
在![]() 上恒成立,
上恒成立,
①∵![]() ,∴
,∴![]() ,即
,即![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
则![]() 在
在![]() 上递减,
上递减, ![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() ;
;
②∵![]() ,∴
,∴![]() ,即
,即![]() ,
, ![]() ,
,
由①得![]() 在
在![]() 上递减,
上递减, ![]() 上递增,又
上递增,又![]() ,
, ![]() 时
时![]() ,∴
,∴![]() ;综上①②可知,
;综上①②可知, ![]() 或
或![]() ;
;
(2)由(1)可知,当![]() 时,
时, ![]() 在
在![]() 上递减,∵
上递减,∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,
,
令![]() ,
, ![]() ,则证
,则证![]() ,令
,令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上递减,又
上递减,又![]() ,∴
,∴![]() ,即
,即![]() ,得证.
,得证.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面积为10
,△ABC的面积为10 ![]() ,求BC边上的中线长.
,求BC边上的中线长. 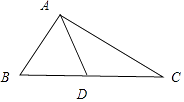
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ].
].
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最大值及单调递增区间.
,求f(x)的最大值及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我省城乡居民社会养老保险个人年缴费分100,200,300,400,500,600,700,800,900,1000(单位:元)十个档次,某社区随机抽取了50名村民,按缴费在100:500元,600:1000元,以及年龄在20:39岁,40:59岁之间进行了统计,相关数据如下:
100﹣500元 | 600﹣1000 | 总计 | |
20﹣39 | 10 | 6 | 16 |
40﹣59 | 15 | 19 | 34 |
总计 | 25 | 25 | 50 |
(1)用分层抽样的方法在缴费100:500元之间的村民中随机抽取5人,则年龄在20:39岁之间应抽取几人?
(2)在缴费100:500元之间抽取的5人中,随机选取2人进行到户走访,求这2人的年龄都在40:59岁之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() .
.
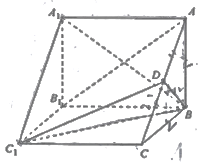
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.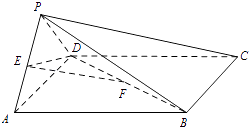
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com