
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在线段
分别在线段 ![]() 上,
上, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.
的中点.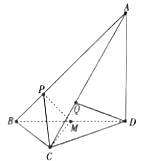
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的大小为
的大小为 ![]() ,求
,求 ![]() .
.
【答案】
(1)证明:取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,所以
,所以 ![]() .
.
又 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
又 ![]() 是
是 ![]() 的中位线,所以
的中位线,所以 ![]() ,
,
从而 ![]() 平面
平面 ![]() .
.
又 ![]() ,所以平面
,所以平面 ![]() 平面
平面 ![]() .
.
因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]()
(2) 解:以 ![]() 为坐标原点,
为坐标原点, ![]() 所在的直线分别为
所在的直线分别为 ![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标.
轴建立如图所示的空间直角坐标.
设 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
,
设 ![]() 是平面
是平面 ![]() 的一个法向量,
的一个法向量,
则  即
即 ![]() 取
取 ![]() ,
,
不难得到平面 ![]() 的一个法向量为
的一个法向量为 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
在 ![]() 中,
中, ![]() .
.

【解析】(1)根据题意作出辅助线利用对应线段成比例性质即可得出线线平行进而得到线面平行,再利用中位线的性质得到线线平行结合线面平行的判定定理即可得证。(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面ABC和平面ABD的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式求出余弦值进而可得到二面角的正切值。
【考点精析】掌握直线与平面平行的判定和平面与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx
(1)当a=1时,求f(x)的单调区间;
(2)若函数f(x)在(0, ![]() )上无零点,求a最小值.
)上无零点,求a最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 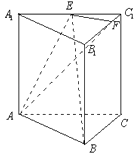
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() :方程
:方程 ![]() 有两个不等的正根;
有两个不等的正根; ![]() :方程
:方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(1)若 ![]() 为真命题,求实数
为真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若“ ![]() 或
或 ![]() ”为真,“
”为真,“ ![]() 且
且 ![]() ”为假,求实数
”为假,求实数 ![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
定价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为 ![]() 件时,销售所得的收入为
件时,销售所得的收入为 ![]() 万元.
万元.
(1)该公司这种产品的年生产量为 ![]() 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量 ![]() 的函数为
的函数为 ![]() ,求
,求 ![]() ;
;
(2)当该公司的年产量为多少件时,当年所获得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com