
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( ) 
| A.0.27,78 | B.0.27,83 | C.2.7,78 | D.2.7,83 |
科目:高中数学 来源: 题型:单选题
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 ( )
| A.588 | B.480 | C.450 | D.120 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.96 | B.模型2的相关指数R2为0.86 |
| C.模型3的相关指数R2为0.73 | D.模型4的相关指数R2为0.66 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
甲、乙两位运动员在5场比赛的得分情况如茎叶图所示,记甲、乙两人的平均得分分别为 ,则下列判断正确的是
,则下列判断正确的是
A.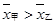 ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
B.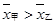 ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
C. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
D. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下图是2013年某市举行的名师评选活动,七位评委为某位教师打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为( )
| 7 | 9 | | | | |
| 8 | 4 | 4 | 6 | 4 | 7 |
| 9 | 3 | | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
200辆汽车通过某一段公路时,时速的频率分布直方图如右图所示,则时速在[50,70)的汽车大约有( ).
A.60辆 B.80辆 C.70辆 D.140辆
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
右表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于( ).
,则a等于( ).
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 5.5 | 5 | 4 | 3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组一次为 若低于60分的人数是15人,则该班的学生人数是( )
若低于60分的人数是15人,则该班的学生人数是( )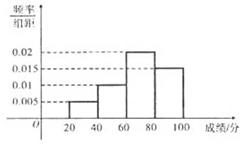
A.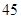 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com