
【题目】已知函数![]()
![]() 的图像两相邻对称轴之间的距离是
的图像两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图像先向右平移
的图像先向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得函数
个单位,所得函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调区间;
的对称轴及单调区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知在一次射击预选赛中,甲、乙两人各射击![]() 次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )
次,两人成绩的条形统计图如图所示,则下列四个选项中判断不正确的是( )

A. 甲的成绩的平均数小于乙的成绩的平均数
B. 甲的成绩的中位数小于乙的成绩的中位数
C. 甲的成绩的方差大于乙的成绩的方差
D. 甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知过原点O的直线与函数![]() 的图象交于A,B两点,分别过A,B作y轴的平行线与函数
的图象交于A,B两点,分别过A,B作y轴的平行线与函数![]() 图象交于C,D两点,若
图象交于C,D两点,若![]() 轴,则四边形ABCD的面积为_____.
轴,则四边形ABCD的面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级一个学习兴趣小组进行社会实践活动,决定对某“著名品牌”![]() 系列进行市场销售量调研,通过对该品牌的
系列进行市场销售量调研,通过对该品牌的![]() 系列一个阶段的调研得知,发现
系列一个阶段的调研得知,发现![]() 系列每日的销售量
系列每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (元/千克)近似满足关系式
(元/千克)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为6元/千克时,每日可售出
为常数.已知销售价格为6元/千克时,每日可售出![]() 系列15千克.
系列15千克.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 系列的成本为4元/千克,试确定销售价格
系列的成本为4元/千克,试确定销售价格![]() 的值,使该商场每日销售
的值,使该商场每日销售![]() 系列所获得的利润最大.
系列所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱台ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2. (Ⅰ)若M为CD中点,求证:AM⊥平面AA1B1B;
(Ⅱ)求直线DD1与平面A1BD所成角的正弦值.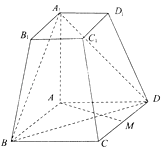
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表中提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的四组对应数据.
(吨标准煤)的四组对应数据.
| 6 | 8 | 10 | 12 |
| 2.5 | 3 | 4 | 4.5 |
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为45吨标准煤,试根据(1)中的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣aex﹣e2x(a∈R,e是自然对数的底数). (Ⅰ)若f(x)≤0对任意x∈R恒成立,求实数a的取值范围;
(Ⅱ)若方程x﹣aex=0有两个不同的实数解x1 , x2 , 求证:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|2x+1|,a∈R.
(1)当a=1时,求不等式f(x)≤1的解集;
(2)设关于x的不等式f(x)≤-2x+1的解集为P,且![]() P,求a的取值范围.
P,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com