
ЁОЬтФПЁПФГАрМЖЦкФЉПМЪдКѓЃЌЖдЪ§бЇГЩМЈдк![]() ЗжвдЩЯЃЈКЌ
ЗжвдЩЯЃЈКЌ![]() ЗжЃЉЕФбЇЩњГЩМЈНјааЭГМЦЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.Цфжа
ЗжЃЉЕФбЇЩњГЩМЈНјааЭГМЦЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.Цфжа![]() ЗжЪ§ЖЮЕФШЫЪ§ЮЊ
ЗжЪ§ЖЮЕФШЫЪ§ЮЊ![]() ШЫ.
ШЫ.
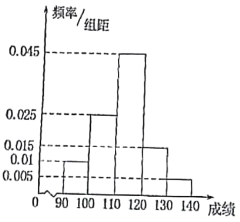
ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЃЌаДГіИУАрМЖбЇЩњЪ§бЇГЩМЈЕФжкЪ§ЃЛ
ЃЈ2ЃЉЯжИљОнбЇЩњЪ§бЇГЩМЈДгЕквЛзщКЭЕкЫФзщЃЈДгЕЭЗжЖЮЕНИпЗжЖЮвРДЮЮЊЕквЛзщЃЌЕкЖўзщЃЌ![]() ЃЌЕкЮхзщЃЉжаШЮвтбЁГіСНШЫаЮГЩбЇЯАаЁзщ.ШєбЁГіЕФСНШЫГЩМЈжЎВюДѓгк
ЃЌЕкЮхзщЃЉжаШЮвтбЁГіСНШЫаЮГЩбЇЯАаЁзщ.ШєбЁГіЕФСНШЫГЩМЈжЎВюДѓгк![]() ЗждђГЦетСНШЫЮЊЁАзюМбзщКЯЁБЃЌЪдЧѓбЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЕФИХТЪ.
ЗждђГЦетСНШЫЮЊЁАзюМбзщКЯЁБЃЌЪдЧѓбЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉжкЪ§ЮЊ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнзюИпОиаЮЕзБпЕФжаЕужЕЮЊжкЪ§ПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉЯШМЦЫуГіЕквЛзщЕФШЫЪ§ЮЊ![]() ЃЌЗжБ№МЧЮЊ
ЃЌЗжБ№МЧЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЕкЫФзщЕФШЫЪ§ЮЊ
ЃЌЕкЫФзщЕФШЫЪ§ЮЊ![]() ЃЌЗжБ№МЧЮЊ
ЃЌЗжБ№МЧЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌСаОйГіЫљгаЕФЛљБОЪТМўЃЌМЧЪТМў
ЃЌСаОйГіЫљгаЕФЛљБОЪТМўЃЌМЧЪТМў![]() бЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЃЌШЗЖЈЪТМў
бЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЃЌШЗЖЈЪТМў![]() ЫљАќКЌЕФЛљБОЪТМўЃЌРћгУЙХЕфИХаЭЕФИХТЪЙЋЪНПЩМЦЫуГіЫљЧѓЪТМўЕФИХТЪ.
ЫљАќКЌЕФЛљБОЪТМўЃЌРћгУЙХЕфИХаЭЕФИХТЪЙЋЪНПЩМЦЫуГіЫљЧѓЪТМўЕФИХТЪ.
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌИУАрМЖбЇЩњЪ§бЇГЩМЈЕФжкЪ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕквЛзщЕФШЫЪ§ЮЊ![]() ЃЌЗжБ№МЧЮЊ
ЃЌЗжБ№МЧЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
ЕкЫФзщЕФШЫЪ§ЮЊ![]() ЃЌЗжБ№МЧЮЊ
ЃЌЗжБ№МЧЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
дкЕквЛзщКЭЕкЫФзщжаШЮвтбЁГіСНШЫаЮГЩбЇЯАаЁзщЃЌЫљгаЕФЛљБОЪТМўгаЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЙВ
ЃЌЙВ![]() жжЃЌ
жжЃЌ
МЧЪТМў![]() бЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЃЌдђЫљбЁЕФСНШЫБиаыЪЧРДздВЛЭЌЕФСНзщЃЌ
бЁГіЕФСНШЫЮЊЁАзюМбзщКЯЁБЃЌдђЫљбЁЕФСНШЫБиаыЪЧРДздВЛЭЌЕФСНзщЃЌ
ЪТМў![]() ЫљАќКЌЕФЛљБОЪТМўгаЃК
ЫљАќКЌЕФЛљБОЪТМўгаЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЙВ
ЃЌЙВ![]() жжЃЌ
жжЃЌ
вђДЫЃЌ![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМКжЊжБЯп2xЉyЉ1=0гыжБЯпxЉ2y+1=0НЛгкЕуPЃЎ
ЃЈЂёЃЉЧѓЙ§ЕуPЧвЦНаагкжБЯп3x+4yЉ15=0ЕФжБЯп![]() ЕФЗНГЬЃЛЃЈНсЙћаДГЩжБЯпЗНГЬЕФвЛАуЪНЃЉ
ЕФЗНГЬЃЛЃЈНсЙћаДГЩжБЯпЗНГЬЕФвЛАуЪНЃЉ
ЃЈЂђЃЉЧѓЙ§ЕуPВЂЧвдкСНзјБъжсЩЯНиОрЯрЕШЕФжБЯп![]() ЗНГЬЃЈНсЙћаДГЩжБЯпЗНГЬЕФвЛАуЪНЃЉ
ЗНГЬЃЈНсЙћаДГЩжБЯпЗНГЬЕФвЛАуЪНЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() ИіШЫХХГЩвЛХХЃЌдкЯТСаЧщПіЯТЃЌИїгаЖрЩйжжВЛЭЌХХЗЈЃП
ИіШЫХХГЩвЛХХЃЌдкЯТСаЧщПіЯТЃЌИїгаЖрЩйжжВЛЭЌХХЗЈЃП
ЃЈ1ЃЉМзВЛдкСНЖЫЃЛ
ЃЈ2ЃЉМзЁЂввЁЂБћШ§ИіБиаыдквЛЦ№ЃЛ
ЃЈ3ЃЉМзЁЂввБиаыдквЛЦ№ЃЌЧвМзЁЂввЖМВЛФмгыБћЯрСкЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁбOЕФжБОЖAB=3ЃЌЕуCЮЊЁбOЩЯвьгкAЃЌBЕФвЛЕуЃЌ![]() ЦНУцABCЃЌЧв
ЦНУцABCЃЌЧв![]() ЃЌЕуMЮЊЯпЖЮVBЕФжаЕу.
ЃЌЕуMЮЊЯпЖЮVBЕФжаЕу.
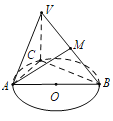
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУцVACЃЛ
ЦНУцVACЃЛ
ЃЈ2ЃЉШєABгыЦНУцVACЫљГЩНЧЕФгрЯвжЕЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
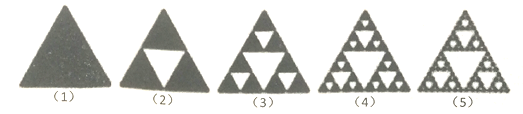
ЁОЬтФПЁПаЛЖћБіЫЙЛљШ§НЧаЮЃЈSierpinski triangleЃЉЪЧвЛжжЗжаЮЃЌгЩВЈРМЪ§бЇМваЛЖћБіЫЙЛљдк1915ФъЬсГі.дквЛИіе§Ш§НЧаЮжаЃЌЭкШЅвЛИіЁАжааФШ§НЧаЮЁБЃЈМДвддШ§НЧаЮИїБпЕФжаЕуЮЊЖЅЕуЕФШ§НЧаЮЃЉЃЌШЛКѓдкЪЃЯТЕФаЁШ§НЧаЮжагжЭкШЅвЛИіЁАжааФШ§НЧаЮЁБЃЌЮвУЧгУАзЩЋШ§НЧаЮДњБэЭкШЅЕФВПЗжЃЌКкЩЋШ§НЧаЮЮЊЪЃЯТЕФВПЗжЃЌЮвУЧГЦДЫШ§НЧаЮЮЊаЛЖћБіЫЙЛљШ§НЧаЮ.ШєдкЭМЃЈ3ЃЉФкЫцЛњШЁвЛЕуЃЌдђДЫЕуШЁздаЛЖћБіЫЙЛљШ§НЧаЮЕФИХТЪЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.Шє![]() ЮЊецУќЬтЃЌдђ
ЮЊецУќЬтЃЌдђ![]() ЃЌ
ЃЌ![]() ОљЮЊМйУќЬтЃЛ
ОљЮЊМйУќЬтЃЛ
B.УќЬтЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБЕФФцЗёУќЬтЮЊецУќЬтЃЛ
ЁБЕФФцЗёУќЬтЮЊецУќЬтЃЛ
C.ЕШБШЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌШєЁА
ЃЌШєЁА![]() ЁБдђЁА
ЁБдђЁА![]() ЁБЕФЗёУќЬтЮЊецУќЬтЃЛ
ЁБЕФЗёУќЬтЮЊецУќЬтЃЛ
D.ЁАЦНУцЯђСП![]() гы
гы![]() ЕФМаНЧЮЊЖлНЧЁБЕФГфвЊЬѕМўЪЧЁА
ЕФМаНЧЮЊЖлНЧЁБЕФГфвЊЬѕМўЪЧЁА![]() ЁБ
ЁБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНЃЈkx+![]() ЃЉexЉ2xЃЌШєfЃЈxЃЉЃМ0ЕФНтМЏжагаЧвжЛгавЛИіе§ећЪ§ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЮЊ ЃЈЁЁЁЁЃЉ
ЃЉexЉ2xЃЌШєfЃЈxЃЉЃМ0ЕФНтМЏжагаЧвжЛгавЛИіе§ећЪ§ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЮЊ ЃЈЁЁЁЁЃЉ
A. [![]() ЃЌ
ЃЌ![]() ЃЉB. ЃЈ
ЃЉB. ЃЈ![]() ЃЌ
ЃЌ![]() ]
]
C. [![]() ЃЉD. [
ЃЉD. [![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊФГАрЙВга![]() ШЫЃЌМЧет
ШЫЃЌМЧет![]() ШЫЩњШежСЩйгаСНШЫЯрЭЌЕФИХТЪЮЊ
ШЫЩњШежСЩйгаСНШЫЯрЭЌЕФИХТЪЮЊ![]() ЃЌ
ЃЌ![]() ЃЌНЋвЛФъПДзї365Ьь.
ЃЌНЋвЛФъПДзї365Ьь.
ЃЈiЃЉЧѓ![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈiiЃЉЙРМЦ![]() ЕФНќЫЦжЕЃЈОЋШЗЕН0.01ЃЉ.
ЕФНќЫЦжЕЃЈОЋШЗЕН0.01ЃЉ.
ВЮПМЪ§жЕЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЃО0ЃЌЧвaЁй1ЃЎУќЬтPЃККЏЪ§fЃЈxЃЉЃНlogaxдкЃЈ0ЃЌ+ЁоЃЉЩЯЮЊдіКЏЪ§ЃЛУќЬтQЃККЏЪ§gЃЈxЃЉЃНx2Љ2ax+4гаСуЕуЃЎ
ЃЈ1ЃЉШєУќЬтPЃЌQТњзуPецQМйЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉУќЬтSЃККЏЪ§yЃНfЃЈgЃЈxЃЉЃЉдкЧјМф[2ЃЌ+ЁоЃЉЩЯжЕКуЮЊе§Ъ§ЃЎШєУќЬтSЮЊецУќЬтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com