
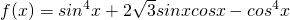
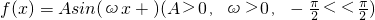 的形式,并写出最小正周期.
的形式,并写出最小正周期.
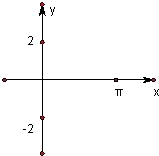
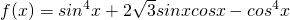 =sin2x-cos2x+
=sin2x-cos2x+ sin2x=
sin2x=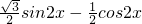 )=2sin(2x-
)=2sin(2x- ).最小正周期为 T=
).最小正周期为 T= =π.
=π.2x- | 0 |  | π |  | 2 π |
| x |  |  |  |  | 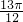 |
| y | 0 | 2 | 0 | -2 | 0 |
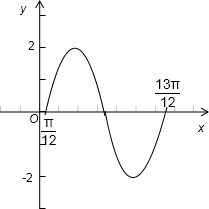
 ],[
],[ ,π].
,π]. 对称,故
对称,故 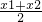 =
= ,∴x1+x2=
,∴x1+x2= .
. 对称,从而有
对称,从而有 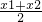 =
= .
.

 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市宝山区行知中学高三(上)期中数学试卷(解析版) 题型:解答题
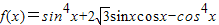
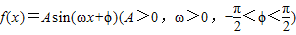 的形式,并写出最小正周期.
的形式,并写出最小正周期.
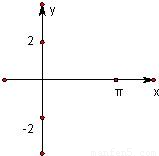
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知函数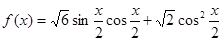
(1)将函数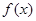 化简成
化简成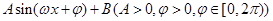 的形式;
的形式;
(2)求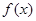 的单调递减区间;
的单调递减区间;
(3)求函数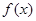 在
在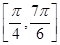 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高一周练数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数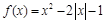 .(1)将函数
.(1)将函数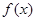 的解析式写成分段函数;
的解析式写成分段函数;
(2)在给出的坐标系中画出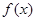 的图象,并根据图象写出函数
的图象,并根据图象写出函数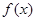 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com