
【题目】如图所示的几何体中,![]() 为三棱柱,且
为三棱柱,且![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() .
.
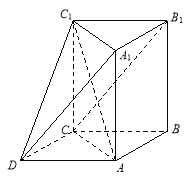
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】设不等式组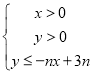 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
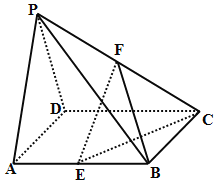
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求三棱锥B-EFC的体积;
(3)求二面角P-EC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为制定初中七、八、九年级学生校服的生产计划,有关部门准备对180名初中男生的身高作调查.
(1)为了达到估计该地初中三个年级男生身高分布的目的,你认为采用怎样的调查方案比较合理?
(2)表中的数据是使用了某种调查方法获得的:七、八、九年级180名男生身高:
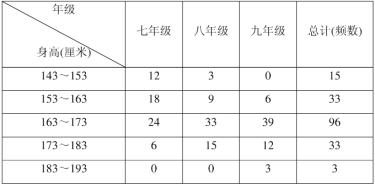
注:表中每组可含最低值,不含最高值.
根据表中的数据,请你给校服生产厂家指定一份生产计划思路.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一段河流,河的一侧是以O为圆心,半径为![]() 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧![]() 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为![]() ,
,![]() 和
和![]() .
.

(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com