
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.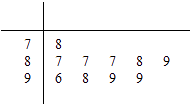
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
【答案】
(1)解:设Ai表示所取3人中有i个人评价该教师为“优秀”,
至多1人评价该教师为“优秀”记为事件A,
则P(A)=P(A0)+P(A1)= ![]() =
= ![]() .
.
(2)解:由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=( ![]() )3=
)3= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)=( ![]() )3=
)3= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =0.9.
=0.9.
【解析】(1)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多1人评价该教师为“优秀”记为事件A,由P(A)=P(A0)+P(A1),能求出至多有1人评价该教师是“优秀”的概率.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.


科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25 ![]() 米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°. 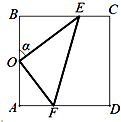
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
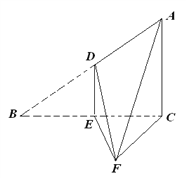
【题目】如图,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1,(a为实数),g(x)=lnx﹣x
(1)讨论函数f(x)的单调区间;
(2)求函数g(x)的极值;
(3)求证:lnx<x<ex(x>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,记
,记![]() ,若数列
,若数列![]() 满足:“存在
满足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,则称数列
”,则称数列![]() 具有性质
具有性质![]() .
.
(Ⅰ)若数列![]() 满足
满足![]() 判断数列
判断数列![]() 是否具有性质
是否具有性质![]() ?是否具有性质
?是否具有性质![]() ?
?
(Ⅱ)求证:“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件;
”的必要不充分条件;
(Ⅲ)已知![]() 是各项为正整数的数列,且
是各项为正整数的数列,且![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,求证:存在整数
,求证:存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米. 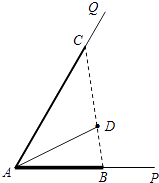
(1)若规划宽长廊AB与窄长廊AC的长度相等,则水上通道AD的总造价需多少万元?
(2)如何设计才能使得水上通道AD的总造价最低?最低总造价是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com