【题目】选修4-5：不等式选讲
已知函数
（Ⅰ）求不等式
的解集；
（Ⅱ）已知函数
的最小值为
，若实数
且
，求
的
最小值．
科目：高中数学 来源： 题型：
【题目】如图，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C．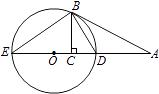
（1）证明：∠CBD=∠DBA；
（2）若AD=3DC，BC= 
，求⊙O的直径．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=asinx﹣bcosx（a，b为常数，a≠0，x∈R）在x= 
处取得最大值，则函数y=f（x+ ）是（ ）
A.奇函数且它的图象关于点（π，0）对称
B.偶函数且它的图象关于点（ 
，0）对称
C.奇函数且它的图象关于点（ ，0）对称
D.偶函数且它的图象关于点（π，0）对称
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a∈R，函数f（x）=xln（﹣x）+（a﹣1）x．
（1）若f（x）在x=﹣e处取得极值，求函数f（x）的单调区间；
（2）求函数f（x）在区间[﹣e2 ， ﹣e﹣1]上的最大值g（a）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的单调函数f（x）满足：f（x+y）=f（x）+f（y），若F（x）=f（asinx）+f（sinx+cos2x﹣3）在（0，π）上有零点，则a的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=x+x2 ．
（1）求x＜0时，f（x）的解析式；
（2）问是否存在这样的非负数a，b，当x∈[a，b]时，f（x）的值域为[4a﹣2，6b﹣6]？若存在，求出所有的a，b值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于数列
， 
， 
， 
，若满足
，则称数列
为“
数列”．
若存在一个正整数
，若数列
中存在连续的
项和该数列中另一个连续的
项恰好按次序对应相等，则称数列
是“
阶可重复数列”，
例如数列
因为
， 
， 
， 
与
， 
， 
， 
按次序对应相等，所以数列
是“
阶可重复数列”．
（I）分别判断下列数列
， 
， 
， 
， 
， 
， 
， 
， 
， 
．是否是“
阶可重复数列”？如果是，请写出重复的这
项；
（II）若项数为
的数列
一定是 “
阶可重复数列”，则
的最小值是多少？说明理由；
（III）假设数列
不是“
阶可重复数列”，若在其最后一项
后再添加一项
或
，均可 使新数列是“
阶可重复数列”，且
，求数列
的最后一项
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x（x+a）﹣lnx，其中a为常数．
（1）当a=﹣1时，求f（x）的极值；
（2）若f（x）是区间 
内的单调函数，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
