
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若二面角
)若二面角![]() 为直二面角,
为直二面角,
(i)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(ii)棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析;(2)(i)![]() ,(ii)见解析.
,(ii)见解析.
【解析】试题分析:(1)连结BD,设AC∩BD=O,设G为DE的中点,连结OG,FG,推导出四边形AOGF为平行四边形,从而AC∥FG,由此能证明AC∥平面DEF.
(2)(i)以A为原点,AD,AB,AF分别为x,y,z轴建立空间直角坐标系,利用向量法能求出直线AC与平面CDE所成角的大小.
(ii)假设棱DE上存在点P,使得BP⊥平面DEF.设![]() ,则
,则![]() ,设P(x,y,z),求出P点坐标为
,设P(x,y,z),求出P点坐标为![]() ,从而
,从而![]() ,由此能求出DE上存在点P,使得BP⊥平面DEF,且
,由此能求出DE上存在点P,使得BP⊥平面DEF,且![]() .
.
试题解析:
(![]() )证明:连接
)证明:连接![]() 交
交![]() 于
于![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() 是
是![]() 中点,
中点,
设![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
, ![]() ,
,
则![]() ,且
,且![]() ,
,
∵四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,即
,即![]() ,
,
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )(i)由已知,
)(i)由已知, ![]() ,
, ![]() ,
,
∴![]() ,
,
∵二面角![]() 为直二面角,
为直二面角,
∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
, ![]() ,
,
又四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示,
由![]() 得:
得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则:
,则:
![]() ,即
,即![]() ,
,
取![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则有:
,则有:
![]() ,
,
∵![]() ,
,
∴![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
(ii)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
解得![]() ,
, ![]() ,
, ![]() ,
,
即![]() 点坐标为
点坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,即
,即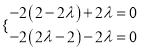 ,
,
解得![]() .
.
∵![]() ,
,
∴![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过点A(0,-b)和B(a,0)的直线与坐标原点距离为
,过点A(0,-b)和B(a,0)的直线与坐标原点距离为![]() .
.
(1)求椭圆的方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆相交于C、D两点,试判断是否存在k值,使以CD为直径的圆过定点E?若存在求出这个k值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=k(x+ ![]() )与曲线y=
)与曲线y= ![]() 恰有两个不同交点,记k的所有可能取值构成集合A;P(x,y)是椭圆
恰有两个不同交点,记k的所有可能取值构成集合A;P(x,y)是椭圆 ![]() 上一动点,点P1(x1 , y1)与点P关于直线y=x+l对称,记
上一动点,点P1(x1 , y1)与点P关于直线y=x+l对称,记 ![]() 的所有可能取值构成集合B,若随机地从集合A,B中分别抽出一个元素λ1 , λ2 , 则λ1>λ2的概率是 .
的所有可能取值构成集合B,若随机地从集合A,B中分别抽出一个元素λ1 , λ2 , 则λ1>λ2的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题13分)已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]()
![]() .记
.记
集合![]() .
.
(Ⅰ)若![]() ,写出集合
,写出集合![]() 的所有元素;
的所有元素;
(Ⅱ)若集合![]() 存在一个元素是3的倍数,证明:
存在一个元素是3的倍数,证明:![]() 的所有元素都是3的倍数;
的所有元素都是3的倍数;
(Ⅲ)求集合![]() 的元素个数的最大值.
的元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率e=
(a>b>0)的离心率e= ![]() ,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为
,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为 ![]()
(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M, ![]() =λ(
=λ( ![]() ),若点N在圆O上,求正实数λ的取值范围.
),若点N在圆O上,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为4的正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将![]() 沿DE,EF,DF折成正四面体
沿DE,EF,DF折成正四面体![]() ,则在此正四面体中,下列说法正确的是______.
,则在此正四面体中,下列说法正确的是______.
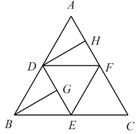
![]() 异面直线PG与DH所成的角的余弦值为
异面直线PG与DH所成的角的余弦值为![]() ;
;
![]() ;
;
![]() 与PD所成的角为
与PD所成的角为![]() ;
;
![]() 与EF所成角为
与EF所成角为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com