
【题目】如图,四棱锥![]() 的底面为菱形,
的底面为菱形,![]() ,
,![]() .平面
.平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() //平面
//平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,证明四边形
,证明四边形![]() 是平行四边形,再利用线面平行判定定理,即可证得结论;
是平行四边形,再利用线面平行判定定理,即可证得结论;
(2)分别以![]() 所在方向为
所在方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的一个法向量
的一个法向量![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,代入公式
,代入公式![]() ,即可得答案;
,即可得答案;
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
![]() 分别是
分别是![]() 的中点,
的中点,![]() ,且
,且![]() ,
,
菱形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,且
,且![]() ,
,
![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.

(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
![]() .
.
∴平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
则![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 中,
中,
![]() .
.
如图,分别以![]() 所在方向为
所在方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,
,

则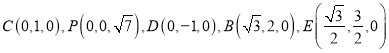 ,
,
 .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
由 得
得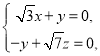
令![]()
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
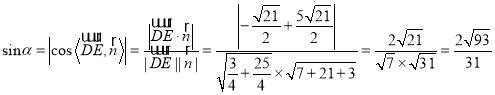 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:![]() )情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
)情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
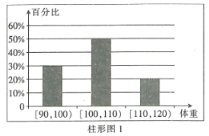
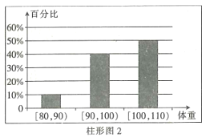
A.他们健身后,体重在区间![]() 内的人数增加了2个
内的人数增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.因为体重在![]() 内所占比例没有发生变化,所以说明健身对体重没有任何影响
内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF中,AB=![]() ,CE=1,CE⊥平面ABCD.
,CE=1,CE⊥平面ABCD.
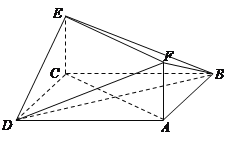
(1)求异面直线DF与BE所成角的余弦值;
(2)求二面角A-DF-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“家校连心,立德树人——重温爱国故事,弘扬爱国主义精神社会课堂”活动中,王老师组建了一个微信群,群的成员由学生、家长、老师和讲解员共同组成.已知该微信群中男学生人数多于女生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数多于讲解员人数,讲解员人数的两倍多于男生人数.若把这5类人群的人数作为一组数据,当该微信群总人数取最小值时,这组数据的中位数是( )
A.5B.6C.7D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为21世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了两款电动汽车车型![]() 和车型
和车型![]() ,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车
,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车![]() 店的销量(单位:台),得到下表:
店的销量(单位:台),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
车型 | 6 | 6 | 13 | 8 | 11 |
车型 | 12 | 9 | 13 | 6 | 4 |
(1)若从甲、乙两家![]() 店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型
店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型![]() 的概率;
的概率;
(2)现从这5家汽车![]() 店中任选3家举行促销活动,用
店中任选3家举行促销活动,用![]() 表示其中车型
表示其中车型![]() 销量超过车型
销量超过车型![]() 销量的
销量的![]() 店的个数,求随机变量
店的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,设
,设![]() 为线段
为线段![]() 的中点.则在
的中点.则在![]() 翻折过程中,给出如下结论:
翻折过程中,给出如下结论:
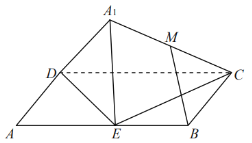
①当![]() 不在平面
不在平面![]() 内时,
内时,![]() 平面
平面![]() ;
;
②存在某个位置,使得![]() ;
;
③线段![]() 的长是定值;
的长是定值;
④当三棱锥![]() 体积最大时,其外接球的表面积为
体积最大时,其外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.(请将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是![]() ,从第二代开始,若上一代开红花,则这一代开红花的概率是
,从第二代开始,若上一代开红花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() ;若上一代开黄花,则这一代开红花的概率是
;若上一代开黄花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() .记第n代开红花的概率为
.记第n代开红花的概率为![]() ,第n代开黄花的概率为
,第n代开黄花的概率为![]() .
.
(1)求![]() ;
;
(2)①证明:数列![]() 为等比数列;
为等比数列;
②第![]() 代开哪种颜色花的概率更大?
代开哪种颜色花的概率更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com