
【题目】已知函数f(x)=(x+1)ex和函数g(x)=(ex﹣a)(x﹣1)2(a>0)(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)判断函数g(x)的极值点的个数,并说明理由;
(3)若函数g(x)存在极值为2a2 , 求a的值.
【答案】
(1)解:∵函数y=(x+1)ex,
∴f′(x)=ex+(x+1)ex=(x+2)ex,
由f′(x)>0得(x+2)ex>0,
即x+2>0,得x>﹣2,即函数的单调增区间为(﹣2,+∞).
由f′(x)<0得x<﹣2,即函数的单调递减区间为(﹣∞,﹣2)
(2)解:g′(x)=ex(x﹣1)2+(ex﹣a)(2x﹣2)=(x﹣1)(xex+ex﹣2a)=(x﹣1)(f(x)﹣2a),
当x<﹣1时,f(x)=(x+1)ex≤0,
①当0<a<e时,由(1)得f(x)在(﹣1,+∞)上单调递增,且f(﹣1)﹣2a<0,f(1)﹣2a=2e﹣2a>0,
则唯一x0∈(﹣1,1),使f(x0)=0,
当x∈(﹣∞,x0)时,f(x)﹣2a<0,故g′(x)>0,
当x∈(x0,1)时,f(x)﹣2a>0,故g′(x)<0,
当x∈(1,+∞)时,f(x)﹣2a>0,故g′(x)>0,
故当x=x0时,函数g(x)取得极大值,当x=1时,函数g(x)取得极小值.
②当a=e时,由(1)得f(x)在(﹣1,+∞)上单调递增,且f(1)﹣2a=0,
当x∈(﹣∞,1)时,f(x)﹣2a<0,故g′(x)>0,
当x∈(1,+∞)时,f(x)﹣2a>0,故g′(x)>0,此时函数g(x)无极值.
③当a>e时,由(1)得f(x)在(﹣1,+∞)上单调递增,且f(1)﹣2a=2e﹣2a<0,
f(lna)﹣2a=a(lna+1)﹣2a=a(lna﹣1)>0,
则唯一x0∈(1,lna),使f(x0)=0,
当x∈(﹣∞,1)时,f(x)﹣2a<0,故g′(x)>0,
当x∈(1,x0)时,f(x)﹣2a<0,故g′(x)<0,
当x∈(x0,+∞)时,f(x)﹣2a>0,故g′(x)>0,
故当x=x0时,函数g(x)取得极小值,当x=1时,函数g(x)取得极大值.
综上当a∈(0,e)∪(e,+∞)时,g(x)有两个极值点,
当a=e时,g(x)无极值点
(3)解:由(2)知当0<a<e时,∵g(1)=0≠ ![]() ,
,
故g(x0)=(e ![]() ﹣a)(x0﹣1)2=2a2,①
﹣a)(x0﹣1)2=2a2,①
由f(x0)=0得a= ![]() ,代入①得(e
,代入①得(e ![]() ﹣
﹣ ![]() )(x0﹣1)2=2[
)(x0﹣1)2=2[ ![]() ]2,
]2,
整理得(1﹣x0)3﹣(1+x0)2e ![]() ﹣=0,
﹣=0,
设h(x)=(1﹣x)3﹣(1+x)2ex,﹣1<x<1,
∵h′(x)=﹣3(1﹣x)2﹣(x+3)(1+x)ex,
∴当﹣1<x<1时,h′(x)<0,
∴h(x)在(﹣1,1)上单调递减,
∵h(0)=0,
∴x0=0,a= ![]() =
= ![]() ∈(0,e)符号题意,
∈(0,e)符号题意,
当a>e时,∵g(x0)<g(1)=0<a2,
∴不存在符号题意的a,
综上当a= ![]() 时,g(x)存在极值等于a2
时,g(x)存在极值等于a2
【解析】(1)求函数的导数,利用函数单调性和导数的关系即可求函数f(x)的单调区间;(2)求函数的导数,根据函数极值和导数的关系即可判断函数g(x)的极值点的个数,并说明理由;(3)根据函数的极值,建立方程关系进行求解即可求a的值.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21. 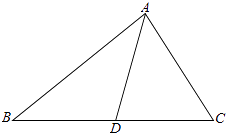
(1)求cos∠B的值;
(2)求sin∠BAC的值和边BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,C在圆O上,CF⊥AB于F,点D为线段CF上任意一点,延长AD交圆O于E,∠AEC=30°. 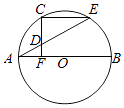
(1)求证:AF=FO;
(2)若CF= ![]() ,求ADAE的值.
,求ADAE的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 的图像在公共点P处有相同的切线,求实数m的值和P的坐标;
的图像在公共点P处有相同的切线,求实数m的值和P的坐标;
(2)若函数![]() 的图像有两个不同的交点M、N,求实数m的取值范围;
的图像有两个不同的交点M、N,求实数m的取值范围;
(3)在(2)的条件下,过线段MN的中点作x轴的垂线分别与![]() 的图像和
的图像和![]() 的图象交于S、T点,以S点为切点作
的图象交于S、T点,以S点为切点作![]() 以T为切点作
以T为切点作![]() 的切线
的切线![]() ,是否存在实数m,使得
,是否存在实数m,使得![]() ?如果存在,求出m的值;如果不存在,请说明理由。
?如果存在,求出m的值;如果不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com