
 如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.
如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.分析 (1)求出函数的导数,求得切线的斜率,可得切线的方程,求得与x轴的交点,可得B1($\frac{4}{3}$,0),A2($\frac{4}{3}$,$\frac{64}{27}$),B2($\frac{8}{9}$,0),A3($\frac{8}{9}$,$\frac{512}{729}$),B3($\frac{16}{27}$,0),即可得到a1,a2,a3,…,由等比数列的通项公式可得通项;
(2)运用两点的距离公式求得线段的长度,再由等比数列的求和公式,计算即可得到所求值.
解答 解:(1)y=x3(x≥0)的导数为y′=3x2,
在点A1(2,8)处的切线斜率为3×4=12,
即有点A1(2,8)处的切线方程为y-8=12(x-2),
令y=0,可得x=$\frac{4}{3}$,即B1($\frac{4}{3}$,0),
由题意可得A2($\frac{4}{3}$,$\frac{64}{27}$),
在点A2处的切线斜率为3×$\frac{16}{9}$=$\frac{16}{3}$,
即有点A2处的切线方程为y-$\frac{64}{27}$=$\frac{16}{3}$(x-$\frac{4}{3}$),
令y=0,可得x=$\frac{8}{9}$,即B2($\frac{8}{9}$,0),
由题意可得A3($\frac{8}{9}$,$\frac{512}{729}$),
在点A3处的切线斜率为3×$\frac{64}{81}$=$\frac{64}{27}$,
即有点A3处的切线方程为y-$\frac{512}{729}$=$\frac{64}{27}$(x-$\frac{8}{9}$),
令y=0,可得x=$\frac{16}{27}$,即B3($\frac{16}{27}$,0),
…,
即有a1=2,a2=$\frac{4}{3}$,a3=$\frac{8}{9}$,…,an=2•($\frac{2}{3}$)n-1;
(2)|B1A2|+|B2A3|+|B3A4|+…+|BnAn+1|
=($\frac{4}{3}$)3+($\frac{8}{9}$)3+($\frac{16}{27}$)3+…+8•($\frac{2}{3}$)3n
=$\frac{\frac{64}{27}(1-\frac{{8}^{n}}{2{7}^{n}})}{1-\frac{8}{27}}$=$\frac{64}{19}$[1-($\frac{8}{27}$)n].
点评 本题考查数列的通项和求和,注意运用归纳法和等比数列的通项公式及求和公式,同时考查导数的运用:求切线的方程,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
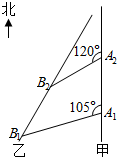 如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里?
如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.
如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\frac{4\sqrt{2}-2}{7}$ | D. | $\frac{4\sqrt{2}+2}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com