
【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“菱草形段”第一个问题“今有菱草六百八十束,欲令‘落一形’捶(同垛)之,问底子(每层三角形边菱草束数,等价于层数)几何?”中探讨了“垛积术”中的落一形垛(“落一形”即是指顶上![]() 束,下一层
束,下一层![]() 束,再下一层
束,再下一层![]() 束,……,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层菱草束数),则本问题中三角垛底层菱草总束数为__________.
束,……,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层菱草束数),则本问题中三角垛底层菱草总束数为__________.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)判断![]() 的形状;
的形状;
(2) 若![]() 两点在抛物线
两点在抛物线![]() 上,点
上,点![]() 满足
满足![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆与抛物线在点
三点的圆与抛物线在点![]() 处的有相同的切线,求点
处的有相同的切线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )

A.120种B.240种C.144种D.288种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某热带风暴中心B位于海港城市A东偏南30°的方向,与A市相距400km.该热带风暴中心B以![]() 的速度向正北方向移动,影响范围的半径是350km.问:从此时起,经多长时间后A市将受热带风暴影响,大约受影响多长时间?
的速度向正北方向移动,影响范围的半径是350km.问:从此时起,经多长时间后A市将受热带风暴影响,大约受影响多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种汽车的元件,该元件是经过![]() 、
、![]() 、
、![]() 三道工序加工而成的,
三道工序加工而成的,![]() 、
、![]() 、
、![]() 三道工序加工的元件合格率分别为
三道工序加工的元件合格率分别为![]() 、
、![]() 、
、![]() .已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
(Ⅰ)生产一个元件,求该元件为二等品的概率;
(Ⅱ)若从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.
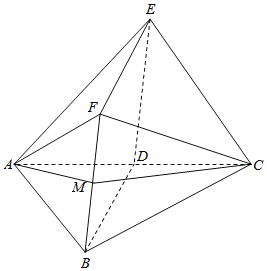
![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com