
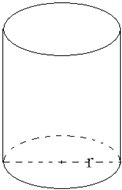
 如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为b千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,高为h(h≥2r),该容器的总建造费用为y千元.
如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为b千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,高为h(h≥2r),该容器的总建造费用为y千元.| V |
| πr2 |
| 2bV |
| r |
| 3 |
| ||
| 2bV |
| r |
| 3 | 2πar2•
| ||||
| 2πa |
| bV |
| r |
| 3 |
| ||


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 某校从高二年级学生中随机抽取40名学生,将他们的期末考试数学成绩(满分为100分,且成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80),[80,90)[,90,100],并将得到的数据如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期末考试数学成绩(满分为100分,且成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80),[80,90)[,90,100],并将得到的数据如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“若x>y,则-x<-y”的逆否命题是“若-x>-y,则x<y” |
| B、若命题P:?x∈R,x2+1>0,则¬P:?x∈R,x2+1>0 |
| C、设l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β |
| D、设x,y∈R,“(x-y)•x2<0”是“x<y”的必要不充分条件. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com