练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝.

    (1)求f(x)的定义域及最小正周期；

    (2)求f(x)的单调递增区间．

     

    （1）π（2）和 (k∈Z)．

    【解析】(1)由sin x≠0得x≠kπ(k∈Z)，

    故f(x)的定义域为{x∈R|x≠kπ，k∈Z}．

    因为f(x)＝

    ＝2cos x(sin x－cos x)

    ＝sin 2x－2cos2x＝sin 2x－(1＋cos 2x)

    ＝ sin－1，

    所以f(x)的最小正周期T＝π.

    (2)由2kπ－≤2x－≤2kπ＋，x≠kπ(k∈Z)，

    得kπ－≤x≤kπ＋，x≠kπ(k∈Z)．

    所以f(x)的单调递增区间为

    和 (k∈Z)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-1练习卷（解析版） 题型：选择题

    已知圆的方程为x2＋y2－6x－8y＝0，设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是(　　)．

    A．10 B．20

    C．30 D．40

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-4-2练习卷（解析版） 题型：填空题

    已知等比数列{an}是递增数列，Sn是{an}的前n项和．若a1，a3是方程x2－5x＋4＝0的两个根，则S6＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-3-2练习卷（解析版） 题型：解答题

    在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2cos B－sin(A－B)sin B＋cos(A＋C)＝－.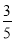

    (1)求cos A的值；

    (2)若a＝4，b＝5，求向量在方向上的投影．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-3-2练习卷（解析版） 题型：选择题

    在△ABC中，角A，B，C所对边的长分别为a，b，c，若a2＋b2＝2c2，则cos C的最小值为(　　)．

    A. B. C. D．－

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-3-1练习卷（解析版） 题型：选择题

    已知ω＞0，函数f(x)＝sin 在上单调递减，则ω的取值范围是(　　)．

    A. 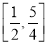B. C. 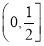D．(0,2]

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-3练习卷（解析版） 题型：填空题

    设直线x＝t，与函数f(x)＝x2，g(x)＝ln x的图象分别交于点M，N，则当|MN|达到最小时t的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-2练习卷（解析版） 题型：选择题

    根据统计，一名工人组装第x件某产品所用的时间(单位：分钟)为f(x)＝ (A，c为常数)．已知工人组装第4件产品用时30分钟，组装第A件产品用时15分钟，那么c和A的值分别是 (　　)．

    A．75,25 B．75,16 C．60,25 D．60,16

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-1-1练习卷（解析版） 题型：选择题

    设U＝R，M＝{x|x2－x≤0}，函数f(x)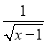＝的定义域为D，则M∩(∁UD)＝(　　)．

    A．[0,1) B．(0,1) C．[0,1] D．{1}

     

    查看答案和解析>>

    同步练习册答案