
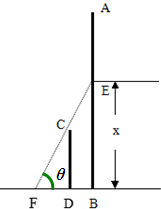
 如图所示,直立在地面上的两根钢管AB和CD,两根钢管相距1m,AB=10
如图所示,直立在地面上的两根钢管AB和CD,两根钢管相距1m,AB=10| 3 |
| 3 |
| DF |
| DF+1 |
3
| ||
| x |
3
| ||
x-3
|
(1+
|
(
|
| 3 |
| 3 |
3
| ||
| sinθ |
| 1 |
| cosθ |
3
| ||
| sinθ |
| 1 |
| cosθ |
| 3 |
3
| ||
| sinθ |
| 1 |
| cosθ |
-3
| ||
| sin2θ |
| sinθ |
| cos2θ |
sin3θ-3
| ||
| sin2θcos2θ |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(1+
|
(
|
| 3 |
| 3 |
| x | ||
x-3
|
| 3 |
| 3 |
(x-3
| ||||
(x-3
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
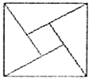 如图所示是曾经在北京召开的国际数学家大会的会标,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
如图所示是曾经在北京召开的国际数学家大会的会标,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 |
| 25 |
| 7 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=
如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
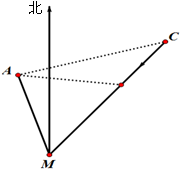 如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?
如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷D(七)(解析版) 题型:解答题
 ,BB1=2.
,BB1=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com