Question

平面α⊥平面β,且α∩β=l,在α内有一个等腰Rt△ABC，∠C=90°,BC在l上，且BC=a，在β内有一条直线CD与α成45°角，P是CD上异于C的一点.

(1)求PB与AC所成的角；

(2)若二面角PABC等于60°，求P点到直线AB的距离.

Answer 1

解:(1)作PH⊥l于H,∵α⊥β，

∴PH⊥平面α.

∴PB在平面α上的射影为BH.

∵BC⊥AC,依三垂线定理知PB⊥AC，

∴PB与AC所成的角为90°.

(2)由(1)知∠PCH为CD与α所成的角，

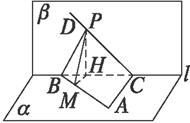
∴∠PCH=45°,△PCH为等腰直角三角形.

作HM⊥AB于M点，连结PM，

由三垂线定理知PM⊥AB,故PM是P点到直线AB的距离，

∠PMH为二面角P-AB-C的平面角.

∴∠PMH=60°.

设PM=x,则在Rt△PHM中，

HM=x,PH=x,CH=x.

∵MH⊥AB,∴△HMB为等腰直角三角形，

HB=HM=x.

∵BH+HC=BC=a，

即x+x=a，

∴x=2(-)a.

∴点P到AB的距离为2(-)a.