【题目】执行如图所示的程序框图，如果输出S=3，那么判断框内应填入的条件是（ ） 
A.k≤6
B.k≤7
C.k≤8
D.k≤9
【答案】B
【解析】解：根据程序框图，运行结果如下：
S k
第一次循环 log23 3
第二次循环 log23log34 4
第三次循环 log23log34log45 5
第四次循环 log23log34log45log56 6
第五次循环 log23log34log45log56log67 7
第六次循环 log23log34log45log56log67log78=log28=3 8
故如果输出S=3，那么只能进行六次循环，故判断框内应填入的条件是k≤7．
故选B．
【考点精析】利用程序框图对题目进行判断即可得到答案，需要熟知程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．
科目：高中数学 来源： 题型：
【题目】如图所示，有两条相交成60°角的直线
，交点为
．甲、乙分别在
上，起初甲离点
，乙离点
，后来甲沿
的方向，乙沿
的方向，同时以
的速度步行．求：
（1）起初两人的距离是多少？
（2）
后两人的距离是多少？
（3）什么时候两人的距离最短？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大型水果超市每天以
元/千克的价格从水果基地购进若干
水果，然后以
元/千克的价格出售，若有剩余，则将剩下的水果以
元/千克的价格退回水果基地，为了确定进货数量，该超市记录了水果最近
天的日需求量（单位：千克），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以天记录的各日需求量的频率代替各日需求量的概率.
（1）求该超市水果日需求量
（单位：千克）的分布列；
（2）若该超市一天购进水果
千克，记超市当天水果获得的利润为
（单位：元），求的分布列及其数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
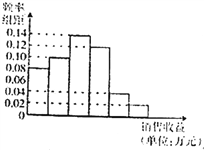
【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入
万元广告费用，并将各地的销售收益（单位：万元）绘制成如图所示的频率分布直方图.由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度；
（Ⅱ）该公司按照类似的研究方法，测得另外一些数据，并整理得到上表：
表中的数据显示
与
之间存在线性相关关系，求关于的回归方程；
（Ⅲ）若广告投入
万元时，实际销售收益为
万元，求残差
.
附：
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin（2ωx+
）+sin（2ωx-）+2cos2ωx，其中ω＞0，且函数f（x）的最小正周期为π
（1）求ω的值；
（2）求f（x）的单调增区间
（3）若函数g（x）=f（x）-a在区间[-
，]上有两个零点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对正整数n，记In={1，2，3…，n}，Pn={ 
|m∈In ， k∈In}．
（1）求集合P7中元素的个数；
（2）若Pn的子集A中任意两个元素之和不是整数的平方，则称A为“稀疏集”．求n的最大值，使Pn能分成两个不相交的稀疏集的并集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）对任意实数x，y恒有f（x+y）＝f（x）+f（y）且当x＞0，f（x）＜0．
给出下列四个结论：
①f（0）＝0； ②f（x）为偶函数；
③f（x）为R上减函数； ④f（x）为R上增函数．
其中正确的结论是（ ）
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
