
����Ŀ����ͼ����������סHС������������C�Ƽ������Ӽҿ�������˾�ϰ�·����L1��L2����·�ߣ�L1·������A1��A2��A3����·�ڣ���·��������Ƶĸ��ʾ�Ϊ ![]() ��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ
��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ ![]() ��
�� ![]() ��
�� 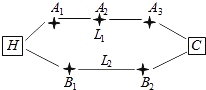
��1������L1·�ߣ����������1�κ�Ƶĸ��ʣ�
��2������L2·�ߣ���������ƴ���X����ѧ������
��3�����ա�ƽ��������ƴ������١���Ҫ�������������������������·����ѡ��һ����õ��ϰ�·�ߣ���˵�����ɣ�
���𰸡�
��1���⣺�衰��L1·���������1�κ�ơ�Ϊ�¼�A������û��������ƺ�ֻ�������һ�����������
�� ![]() ��
��
������L1·�ߣ��������1�κ�Ƶĸ���Ϊ ![]() ��
��
��2���⣺�����⣬X�Ŀ���ȡֵΪ0��1��2��
![]() ��
�� ![]() ��
�� ![]() ��
��
�������X�ķֲ���Ϊ��
X | 0 | 1 | 2 |
P |
|
|
|
���� ![]()
��3���⣺��ѡ��L1·��������ƴ���ΪY���������Y���Ӷ���ֲ�Y�� ![]() ������
������ ![]() ��
��
��ΪEX��EY������ѡ��L2·���ϰ����
����������1�����ö���ֲ����ɵó�����2������������¼��ĸ��ʼ��㹫ʽ����ɢ������������������㹫ʽ���ɵó�����3��������·��L1ʱ���Ӷ���ֲ����ɵó��������Ƚ�������·����ѧ�����Ĵ�С���ɵó�Ҫѡ���·�ߣ�


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ������������ˮ�أ����ݻ�Ϊ6400�����ף����Ϊ4�ף��ص�ÿƽ�������Ϊ120Ԫ���ر�ÿƽ�������Ϊ100Ԫ����ص׳����εij�Ϊx�ף� ���������������ú�x�ı���ʽ��ʾ�ر������
�����������ˮ����ʹ�������ͣ��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
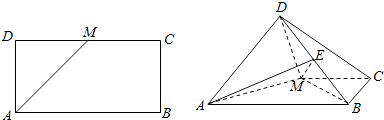
����Ŀ����ͼ����֪������ABCD�У�AB=2 ![]() ��AD=
��AD= ![]() ��MΪDC���е㣬����ADM��AM����ʹ��ƽ��ADM��ƽ��ABCM ������֤��AD��BM
��MΪDC���е㣬����ADM��AM����ʹ��ƽ��ADM��ƽ��ABCM ������֤��AD��BM
��������E���߶�DB�ϵ�һ���㣬�ʵ�E�ں�λ��ʱ�������E��AM��D������ֵΪ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ȳ�������3n+1���룬��ָ����ÿһ������������������������������3�ټ�1���������ż�������������2�����ѭ�������ն��ܵõ�1���Ķ���ͼ��ʾ�ij����ͼ��������Ӧ��������Ľ��i=�� �� 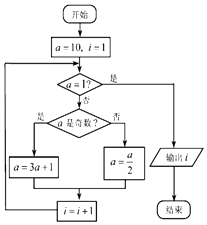
A.4
B.5
C.6
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() �Ķ�������[a��b]��a��bΪ��������ֵ����[0��1]���������������������ԣ�a��b������ ����
�Ķ�������[a��b]��a��bΪ��������ֵ����[0��1]���������������������ԣ�a��b������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ ![]() ����ΪF1 �� �ҽ���ΪF2 �� ��F1��ֱ�߽���Բ��A��B���㣬��ABF2���ܳ�Ϊ8���ҡ�AF1F2������ʱ����AF1F2Ϊ�������Σ�
����ΪF1 �� �ҽ���ΪF2 �� ��F1��ֱ�߽���Բ��A��B���㣬��ABF2���ܳ�Ϊ8���ҡ�AF1F2������ʱ����AF1F2Ϊ�������Σ� 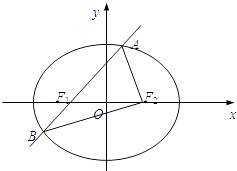
��1������ԲE�ķ��̣�
��2���趯ֱ��l��y=kx+m����ԲE����ֻ��һ��������P������ֱ��x=4�ཻ�ڵ�Q����̽��������PQΪֱ����Բ��x���λ�ù�ϵ�� ��������ƽ�����Ƿ���ڶ���M��ʹ����PQΪֱ����Բ�����M�������ڣ����M�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���ͼ��ʾ�ij����ͼ�������������Ϊ58�����жϿ���Ӧ���������Ϊ�� �� 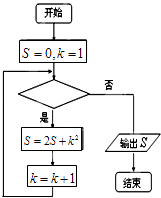
A.k��3
B.k��4
C.k��5
D.k��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
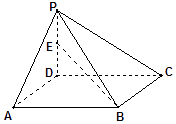
����Ŀ����ͼ��������P��ABCD�У�����ABCD�������Σ�EΪPD�е㣬�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ����
���� ![]() =�� ��
=�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У���С������Ϊ����Ϊ�溯�����ǣ� ��
A.y=sin ![]()
B.y=cos ![]()
C.y=cos2x
D.y=sin2x
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com