
【题目】已知函数![]() ,
,
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)存在正实数k使得函数![]() 有三个零点,求实数a的取值范围.
有三个零点,求实数a的取值范围.
【答案】(Ⅰ)![]() 时增区间为
时增区间为![]() ;
;![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)先求出函数的定义域和导函数,分![]() 和
和![]() 讨论导函数的符号,即可求得函数的单调区间;
讨论导函数的符号,即可求得函数的单调区间;
(Ⅱ)由题易知![]() ,函数
,函数![]() 有三个零点等价于
有三个零点等价于![]() 有三个解,即
有三个解,即![]() 仅有三解,利用分离参数法求解即可.
仅有三解,利用分离参数法求解即可.
(Ⅰ)![]() (
(![]() ),
),
①当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() 得:
得:![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
综上,![]() 时,
时,![]() 的增区间为
的增区间为![]() ,
,
![]() 时,
时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
(Ⅱ)由题易知![]() ,
,
即![]() 有三个解,
有三个解,![]() ,
,
即![]() 仅有三解,
仅有三解,
设![]() ,
,![]() ,
,
![]() 可得
可得![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,![]() 得
得![]() ,
,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() 时,
时,![]() ,
,![]() 单调递减(同时注意
单调递减(同时注意![]() 时,
时,![]() ),
),
![]() ,
,
当![]() 时,
时,![]() 恒成立,此时
恒成立,此时![]() 均符合条件,
均符合条件,
当![]() 时,
时,![]() 由两个根不妨设为
由两个根不妨设为![]() ,
,![]() 且
且![]() ,
,
![]() 有两根,不妨设为
有两根,不妨设为![]() ,
,![]() 则
则![]() ,
,![]() ,则
,则![]() ,
,
容易分析出![]() 在
在![]() ,
,![]() 单调递增,
单调递增,![]() 单调递减,
单调递减,
则当![]() 时
时![]() ,
,
这里需要求![]() 和
和![]() 的取值范围,
的取值范围,
由上面分析可得![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
易知![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() ,∴
,∴![]() ,
,
同理![]() ,
,![]() ,
,
由上面分析![]() 在
在![]() 单调递减,且
单调递减,且![]() 时,
时,![]() ,
,
∴![]() . ∴
. ∴![]() ,
,
综上:![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
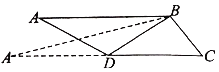
【题目】如图,△ABC中,AB⊥BC,∠ACB=60°,D为AC中点,△ABD沿BD翻折过程中,直线AB与直线BC所成的最大角、最小角分别记为α1,β1,直线AD与直线BC所成最大角、最小角分别记为α2,β2,则有( )
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆![]() 的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与曲线
与曲线![]() 的公共弦所在直线为l.
的公共弦所在直线为l.
(1)在直角坐标系下,求曲线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)若以坐标原点为中心,直线l顺时针方向旋转![]() 后与曲线
后与曲线![]() 、曲线
、曲线![]() 分别在第一象限交于A、B两点,求
分别在第一象限交于A、B两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com