
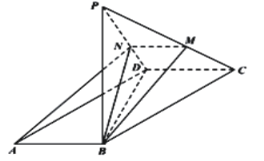
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,现沿对角线
,现沿对角线![]() 将
将![]() 折起,使点A到达点P,点M,N分别在直线
折起,使点A到达点P,点M,N分别在直线![]() ,
,![]() 上,且A,B,M,N四点共面.
上,且A,B,M,N四点共面.
(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小为
平面角大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据余弦定理,可得![]() ,利用
,利用![]() //
//![]() ,可得
,可得![]() //平面
//平面![]() ,然后利用线面平行的性质定理,
,然后利用线面平行的性质定理,![]() //
//![]() ,最后可得结果.
,最后可得结果.
(2)根据二面角![]() 平面角大小为
平面角大小为![]() ,可知N为
,可知N为![]() 的中点,然后利用建系,计算
的中点,然后利用建系,计算![]() 以及平面
以及平面![]() 的一个法向量,利用向量的夹角公式,可得结果.
的一个法向量,利用向量的夹角公式,可得结果.
(1)不妨设![]() ,则
,则![]() ,
,
在![]() 中,
中,
![]() ,
,
则![]() ,
,
因为![]() ,
,
所以![]() ,因为
,因为![]() //
//![]() ,
,
且A、B、M、N四点共面,所以![]() //平面
//平面![]() .
.
又平面![]() 平面
平面![]() ,所以
,所以![]() //
//![]() .
.
而![]() ,
,![]() .
.
(2)因为平面![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
因为![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,
,
所以![]() ,在
,在![]() 中,易知N为
中,易知N为![]() 的中点,
的中点,
如图,建立空间直角坐标系,
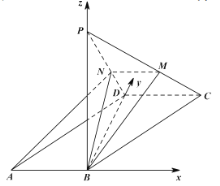
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由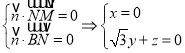 ,
,
令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则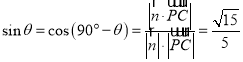 .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线C:x2=4y的准线上任意一点P作抛物线的切线PA,PB,切点分别为A,B,则A点到准线的距离与B点到准线的距离之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 过点
过点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为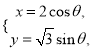 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)过点![]() 与直线
与直线![]() 平行的直线
平行的直线![]() 与曲线
与曲线 ![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某亲子公园拟建议广告牌,将边长为![]() 米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等
米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等![]() 不计焊接点大小
不计焊接点大小![]()

![]() 若
若![]() 时,求焊接点A离地面距离;
时,求焊接点A离地面距离;
![]() 若记
若记![]() ,求加强钢管AN最长为多少?
,求加强钢管AN最长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
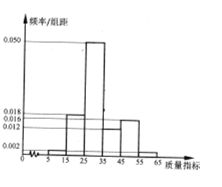
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com