
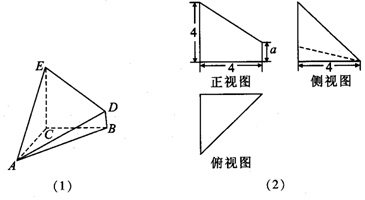
分析 (1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,利用几何体A-BCED的体积为16,求实数a的值;
(2)过B作AD的垂线BH,垂足为H,得BH=$\frac{4\sqrt{2}}{3}$,求出圆锥底面周长,两个圆锥的母线长,即可求该旋转体的表面积.
解答 解:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,
体积V=$\frac{1}{3}•4•\frac{(a+4)×4}{2}$=16,
解得a=2;
(2)在RT△ABD中,AB=4$\sqrt{2}$,BD=2,AD=6,
过B作AD的垂线BH,垂足为H,得BH=$\frac{4\sqrt{2}}{3}$,
该旋转体由两个同底的圆锥构成,圆锥底面半径为BH=$\frac{4\sqrt{2}}{3}$,
所以圆锥底面周长为C=2π•B$\frac{4\sqrt{2}}{3}$=$\frac{8\sqrt{2}π}{3}$,两个圆锥的母线长分别为4$\sqrt{2}$,2,
故该旋转体的表面积为$S=\frac{1}{2}×\frac{8\sqrt{2}π}{3}×(2+4\sqrt{2})$=$\frac{(32+8\sqrt{2})π}{3}$.
点评 本题考查了圆锥的侧面积公式、积体公式和解三角形等知识,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg2•lg3=lg5 | B. | 若sinθ=$\frac{1}{2}$,则θ=30° | ||
| C. | $\root{n}{{a}^{n}}$=a | D. | logax-logay=loga$\frac{x}{y}$(x>0,y>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的实部为2 | B. | z的虚部为i | C. | $\overline z=1+i$ | D. | |z|=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1] | B. | [-2,-1] | C. | (-1,1] | D. | [-1,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com