
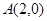 ,
,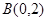 ,
,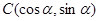 ,
,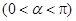 .
.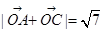 (
(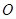 为坐标原点),求
为坐标原点),求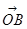 与
与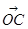 的夹角;
的夹角;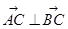 ,求
,求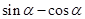 的值.
的值.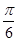 ;(2)
;(2)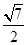
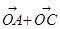 =(2+cosα,sinα),(
=(2+cosα,sinα),(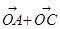 )2=7,∴(2+cosα)2+sin2α=7,∴cosα=
)2=7,∴(2+cosα)2+sin2α=7,∴cosα=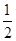 . 又B(0,2),C(cosα,sinα),设
. 又B(0,2),C(cosα,sinα),设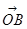 与
与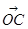 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=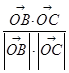 =sinα=±
=sinα=±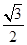 ,∴
,∴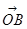 与
与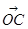 的夹角为
的夹角为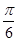 或
或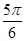 ,又
,又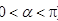 ,∴
,∴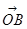 与
与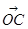 的夹角为
的夹角为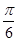 ;
;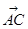 =(cosα-2,sinα),
=(cosα-2,sinα),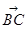 =(cosα,sinα-2),由
=(cosα,sinα-2),由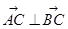 ,∴
,∴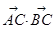 =0,可得cosα+sinα=
=0,可得cosα+sinα=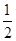 ,∴(cosα+sinα)2=
,∴(cosα+sinα)2=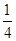 ,∴2sinαcosα=-
,∴2sinαcosα=-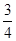 ,∵α∈(0,π),∴α∈(
,∵α∈(0,π),∴α∈(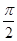 ,π),又由(sinα-cosα)2=1-2sinαcosα=
,π),又由(sinα-cosα)2=1-2sinαcosα=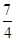 ,sinα-cosα>0,∴sinα-cosα=
,sinα-cosα>0,∴sinα-cosα=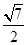


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:不详 题型:解答题
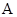 、
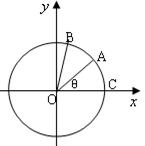
、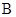 是单位圆上的动点,
是单位圆上的动点,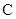 是单位圆与
是单位圆与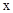 轴的正半轴的交点,且
轴的正半轴的交点,且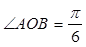 ,记
,记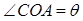 ,
,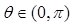 ,
,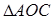 的面积为
的面积为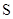 .
.
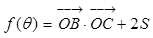 ,试求
,试求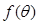 的最大值以及此时
的最大值以及此时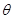 的值.
的值.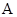 点坐标为
点坐标为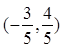 时,求
时,求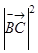 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com