
分析 (1)方法一:化简分段函数,分段求解方程的根即可,方法二:当a=-1时,利用f(x)=1化简求解即可.
(2)化简分段函数,通过当x≥a时,当x<a时,求出函数的零点,推出${x_1}+{x_2}+{x_3}=a+2+\frac{{a-\sqrt{{a^2}-12a}}}{2}=\frac{3a}{2}-\frac{{\sqrt{{{(a-6)}^2}-36}}}{2}+2$,构造函数,利用函数的单调性,求解即可.
解答 解:(1)方法一:
当a=-1时,$f(x)=(x-1)|x+1|-x+2=\left\{\begin{array}{l}{x^2}-x+1,x≥-1\\-{x^2}-x+3,x<-1\end{array}\right.$(2 分)
由f(x)=1得$\left\{\begin{array}{l}x≥-1\\{x^2}-x+1=1\end{array}\right.$或$\left\{\begin{array}{l}x<-1\\-{x^2}-x+3=1\end{array}\right.$(2 分)
解得 x=0,1,-2,即解集为{0,1,-2}. (2分)
方法二:当a=-1时,由f(x)=1得:(x-1)|x+1|-(x-1)=0(x-1)(|x+1|-1)=0(3分)
∴得x=1或|x+1|=1∴x=1或x=0或x=-2
即解集为{0,1,-2}. (3分)
(2)$f(x)=(x-1)|x-a|-x-2a=\left\{\begin{array}{l}{x^2}-(a+2)x-a,x≥a\\-{x^2}+ax-3a,x<a\end{array}\right.$
当x≥a时,令x2-(a+2)x-a=0,∵$a∈(-\frac{1}{2},0)$,
∴△=a2+8a+4=(a+4)2-12>0
得${x_1}=\frac{{(a+2)-\sqrt{{a^2}+8a+4}}}{2}$,${x_2}=\frac{{(a+2)+\sqrt{{a^2}+8a+4}}}{2}$(2分)
且${x_1}-a=\frac{{(a+2)-\sqrt{{a^2}+8a+4}}}{2}-a=\frac{{2-a-\sqrt{{a^2}+8a+4}}}{2}$
先判断2-a,与$\sqrt{{a^2}+8a+4}$大小:∵${(2-a)^2}-({a^2}+8a+4)=-12a>0∴(2-a)>\sqrt{{a^2}+8a+4}$${x_1}-a=\frac{{2-a-\sqrt{{a^2}+8a+4}}}{2}>0$,即a<x1<x2,故当x≥a时,f(x)存在两个零点.(2分)
当x<a时,令-x2+ax-3a=0,即x2-ax+3a=0得∵$a∈(-\frac{1}{2},0)$,
∴△=a2-12a=(a-6)2-36>0
得${x_3}=\frac{{a-\sqrt{{a^2}-12a}}}{2}$,${x_4}=\frac{{a+\sqrt{{a^2}-12a}}}{2}$
同上可判断x3<a<x4,故x<a时,f(x)存在一个零点.(2分)
综上可知当$a∈(-\frac{1}{2},0)$时,f(x)存在三个不同零点.
且${x_1}+{x_2}+{x_3}=a+2+\frac{{a-\sqrt{{a^2}-12a}}}{2}=\frac{3a}{2}-\frac{{\sqrt{{{(a-6)}^2}-36}}}{2}+2$
设$g(a)=\frac{3a}{2}-\frac{{\sqrt{{{(a-6)}^2}-36}}}{2}+2$,易知g(a)在$a∈(-\frac{1}{2},0)$上单调递增,
故g(a)∈(0,2)∴x1+x2+x3∈(0,2). ( 2分)
点评 本题考查函数与方程的综合应用,函数的零点以及函数的单调性的应用,考查分析问题解决问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
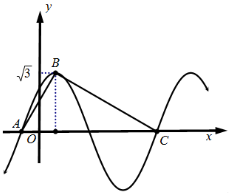 已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).
已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{7}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
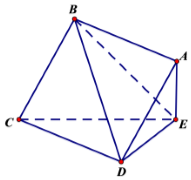 如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com