
【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
[85,95) | ① | 0.025 |
[95,105) | 0.050 | |
[105,115) | 0.200 | |
[115,125) | 12 | 0.300 |
[125,135) | 0.275 | |
[135,145) | 4 | ② |
[145,155] | 0.050 | |
合计 | ③ |
(1)根据图表,①②③处的数值分别为、、;
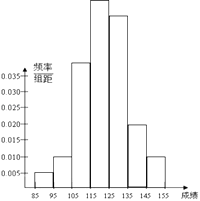
(2)在所给的坐标系中画出[85,155]的频率分布直方图; 
(3)根据题中信息估计总体落在[125,155]中的概率.
【答案】
(1)1;0.1;1
(2)
(3)解:根据题中信息估计总体落在[125,155]中的概率为:
0.275+0.100+0.050=0.425.
【解析】解:(1)∵数学成绩落在区间[115,125)的频数为12,频率为0.300,∴参与抽查的样本容量为 ![]() =40,由于合计的频率和一定为1,故③应填1;由数学成绩落在区间[135,145)的频数为4,可得其频率为
=40,由于合计的频率和一定为1,故③应填1;由数学成绩落在区间[135,145)的频数为4,可得其频率为 ![]() =0.100,故②应填0.1;由于[85,95)的频率为0.025,∴
=0.100,故②应填0.1;由于[85,95)的频率为0.025,∴ ![]() ,解得①处应填1.所以答案是:1,0.1,1.
,解得①处应填1.所以答案是:1,0.1,1.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且cosAcosC﹣cos(A+C)=sin2B. (Ⅰ)证明:a,b,c成等比数列;
(Ⅱ)若角B的平分线BD交AC于点D,且b=6,S△BAD=2S△BCD , 求BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:(k﹣1)x﹣2y+5﹣3k=0(k∈R)恒过定点P,圆C经过点A(4,0)和点P,且圆心在直线x﹣2y+1=0上.
(1)求定点P的坐标;
(2)求圆C的方程;
(3)已知点P为圆C直径的一个端点,若另一个端点为点Q,问:在y轴上是否存在一点M(0,m),使得△PMQ为直角三角形,若存在,求出m的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是梯形,四边形
是梯形,四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的动点.
上的动点.

(1)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)在(1)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA= ![]() ,c=3b,且△ABC面积S△ABC=
,c=3b,且△ABC面积S△ABC= ![]() .
.
(1)求边b.c;
(2)求边a并判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有8名奥运会志愿者,其中志愿者A1 , A2 , A3通晓日语,B1 , B2 , B3通晓俄语,C1 , C2通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求A1被选中的概率;
(2)求B1和C1不全被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com