Question

13．在四边形ABCD中，设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{c}$，则$\overrightarrow{CD}$等于（　　）

• A． $\overrightarrow{c}$-（$\overrightarrow{a}$+$\overrightarrow{b}$）
• B． $\overrightarrow{b}$-（$\overrightarrow{a}+\overrightarrow{c}$）
• C． $\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$
• D． $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$

Answer 1

分析 作出四边形ABCD，结合向量加法法则利用数形结合思想求解．

解答 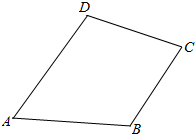解：∵在四边形ABCD中，设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{c}$，
∴$\overrightarrow{c}-（\overrightarrow{a}+\overrightarrow{b}）$=$\overrightarrow{AD}+\overrightarrow{BA}+\overrightarrow{CB}$=$\overrightarrow{CD}$，故A正确；
当四边形ABCD为平行四边形时，
$\overrightarrow{b}-（\overrightarrow{a}+\overrightarrow{c}）$=$\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{DA}$=$\overrightarrow{AB}=-\overrightarrow{CD}$，故B不成立；
$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{DA}$=$\overrightarrow{DC}$，故C错误；
当四边形ABCD为平行四边形时，
$\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$=$\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{AD}$=$\overrightarrow{AB}=-\overrightarrow{CD}$，故D不成立．
故选：A．

点评 本题考查向量的求法，是基础题，解题时要认真审题，注意数形结合思想和向量加法法则的合理运用．