
| AЃЎ | 16 | BЃЎ | -16 | CЃЎ | a2+2a-16 | DЃЎ | a2-2a-16 |
ЗжЮі зїВюfЃЈxЃЉ-gЃЈxЃЉ=2x2-4ax+2a2-8=2ЃЈx-a-2ЃЉЃЈx-a+2ЃЉЃЌДгЖјЛЏМђH1ЃЈxЃЉгыH2ЃЈxЃЉЃЌДгЖјНсКЯЖўДЮКЏЪ§ЕФаджЪЧѓзюжЕЃЌДгЖјНтЕУЃЎ
НтД№ НтЃКfЃЈxЃЉ-gЃЈxЃЉ=2x2-4ax+2a2-8=2ЃЈx-a-2ЃЉЃЈx-a+2ЃЉЃЌ
ЙЪЕБxЁнa+2ЛђxЁмa-2ЪБЃЌfЃЈxЃЉЁнgЃЈxЃЉЃЛ
ЕБa-2ЃМxЃМa+2ЪБЃЌfЃЈxЃЉЃМgЃЈxЃЉЃЌ
ЁпH1ЃЈxЃЉ=$\left\{\begin{array}{l}{fЃЈxЃЉЃЌfЃЈxЃЉЁнgЃЈxЃЉ}\\{gЃЈxЃЉЃЌfЃЈxЃЉЃМgЃЈxЃЉ}\end{array}\right.$ЃЌH2ЃЈxЃЉ=$\left\{\begin{array}{l}{gЃЈxЃЉЃЌfЃЈxЃЉЁнgЃЈxЃЉ}\\{fЃЈxЃЉЃЌfЃЈxЃЉЃМgЃЈxЃЉ}\end{array}\right.$ЃЌ
ЁрH1ЃЈxЃЉ=$\left\{\begin{array}{l}{{x}^{2}-2ЃЈa+2ЃЉx+{a}^{2}ЃЌxЁнa+2ЛђxЁмa-2}\\{-{x}^{2}+2ЃЈa-2ЃЉx-{a}^{2}+8ЃЌa-2ЃМxЃМa+2}\end{array}\right.$ЃЌ
H2ЃЈxЃЉ=$\left\{\begin{array}{l}{-{x}^{2}+2ЃЈa-2ЃЉx-{a}^{2}+8ЃЌa-2ЁмxЁмa+2}\\{{x}^{2}-2ЃЈa+2ЃЉx+{a}^{2}ЃЌxЃОa+2ЛђxЃМa-2}\end{array}\right.$ЃЌ
НсКЯЖўДЮКЏЪ§ЕФаджЪПЩжЊЃЌ
A=H1ЃЈa+2ЃЉ=ЃЈa+2ЃЉ2-2ЃЈa+2ЃЉЃЈa+2ЃЉ+a2=-4a-4ЃЌ
B=H1ЃЈa-2ЃЉ=-ЃЈa-2ЃЉ2+2ЃЈa-2ЃЉЃЈa-2ЃЉ-a2+8=-4a+12ЃЌ
ЙЪA-B=-4a-4-ЃЈ-4a+12ЃЉ=-16ЃЌ
ЙЪбЁBЃЎ
ЕуЦР БОЬтПМВщСЫЗжЖЮКЏЪ§ЕФгІгУМАЖўДЮКЏЪ§ЕФгІгУЃЌЭЌЪБПМВщСЫЗжРрЬжТлЕФЫМЯыгІгУЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
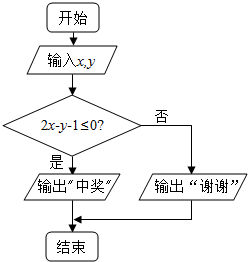 ФГЕЅЮЛГщНБЛюЖЏЕФЙцдђЪЧЃКДњБэЭЈЙ§ВйзїАДМќЪЙЕчФдздЖЏВњЩњСНИі[0ЃЌ1]жЎМфЕФОљдШЫцЛњЪ§xЃЌyЃЌВЂАДШчЭМЫљЪОЕФГЬађПђЭМжДааЃЎШєЕчФдЯдЪОЁАжаНБЁБЃЌдђИУДњБэжаНБЃЛШєЕчФдЯдЪОЁАаЛаЛЁБЃЌдђВЛжаНБЃЌдђИУДњБэжаНБЕФИХТЪЮЊЃЈЁЁЁЁЃЉ
ФГЕЅЮЛГщНБЛюЖЏЕФЙцдђЪЧЃКДњБэЭЈЙ§ВйзїАДМќЪЙЕчФдздЖЏВњЩњСНИі[0ЃЌ1]жЎМфЕФОљдШЫцЛњЪ§xЃЌyЃЌВЂАДШчЭМЫљЪОЕФГЬађПђЭМжДааЃЎШєЕчФдЯдЪОЁАжаНБЁБЃЌдђИУДњБэжаНБЃЛШєЕчФдЯдЪОЁАаЛаЛЁБЃЌдђВЛжаНБЃЌдђИУДњБэжаНБЕФИХТЪЮЊЃЈЁЁЁЁЃЉ| AЃЎ | $\frac{1}{2}$ | BЃЎ | $\frac{1}{3}$ | CЃЎ | $\frac{3}{4}$ | DЃЎ | $\frac{2}{3}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 3Лђ-1 | BЃЎ | 0Лђ-1 | CЃЎ | -3Лђ-1 | DЃЎ | 0Лђ3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {1ЃЌ$\frac{1}{2}$} | BЃЎ | {1ЃЌ2} | CЃЎ | {0ЃЌ1ЃЌ2} | DЃЎ | вдЩЯЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
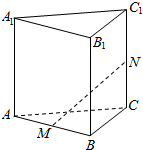 ШчЭМЃЌШ§РтжљABC-A1B1C1ЕФРтГЄЖМЪЧ1ЃЌЁЯBAC=ЁЯBAA1=ЁЯCAA1=60ЁуЃЌЕуMЃЌNЗжБ№ЪЧABЃЌCC1ЕФжаЕуЃЌМЧ$\overrightarrow{AB}$=aЃЌ$\overrightarrow{AC}$=bЃЌ$\overrightarrow{A{A}_{1}}$=cЃЎ
ШчЭМЃЌШ§РтжљABC-A1B1C1ЕФРтГЄЖМЪЧ1ЃЌЁЯBAC=ЁЯBAA1=ЁЯCAA1=60ЁуЃЌЕуMЃЌNЗжБ№ЪЧABЃЌCC1ЕФжаЕуЃЌМЧ$\overrightarrow{AB}$=aЃЌ$\overrightarrow{AC}$=bЃЌ$\overrightarrow{A{A}_{1}}$=cЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
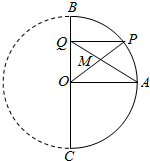 ШчЭМЃЌBCЪЧАыдВЕФжБОЖЃЌOЪЧдВаФЃЌOAЪЧгыBCДЙжБЕФдВЕФАыОЖЃЌPЮЊАыдВЩЯвЛЕуЃЈPгыAЁЂBЁЂCВЛжиКЯЃЉЃЎЙ§PЯђBCзїДЙЯпЃЌДЙзуЮЊQЃЎOPКЭAQЕФНЛЕуЮЊMЃЎЪдЮЪЃКЕБPвЦЖЏЪБЃЌMЕФЙьМЃЪЧдѕбљЕФЧњЯпЃПЫЕУїРэгЩЃЎ
ШчЭМЃЌBCЪЧАыдВЕФжБОЖЃЌOЪЧдВаФЃЌOAЪЧгыBCДЙжБЕФдВЕФАыОЖЃЌPЮЊАыдВЩЯвЛЕуЃЈPгыAЁЂBЁЂCВЛжиКЯЃЉЃЎЙ§PЯђBCзїДЙЯпЃЌДЙзуЮЊQЃЎOPКЭAQЕФНЛЕуЮЊMЃЎЪдЮЪЃКЕБPвЦЖЏЪБЃЌMЕФЙьМЃЪЧдѕбљЕФЧњЯпЃПЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com